题目内容
水平放置的两块平金属板长L,两板间距d,两板间电压为U,且上板为正,一个质量m为带电量为q粒子沿水平方向以速度Vo,从两板中间射入,如图所示,求:
(1)粒子偏离金属板时侧位移OM是多少?
(2)粒子飞出电场时的速度?
(3)粒子离开电场后,打在屏上的P点,若金属板距屏为s,求OP之长.
(1)粒子偏离金属板时侧位移OM是多少?
(2)粒子飞出电场时的速度?
(3)粒子离开电场后,打在屏上的P点,若金属板距屏为s,求OP之长.

分析:(1)粒子进入金属板间做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,根据类平抛运动规律求粒子偏离金属板时侧位移OM.
(2)由类平抛运动的规律求出粒子飞出电场时竖直分速度,再进行合成,即可求解.
(3)求出粒子飞出电场时偏向角的正切,由数学知识求解OP之长.
(2)由类平抛运动的规律求出粒子飞出电场时竖直分速度,再进行合成,即可求解.
(3)求出粒子飞出电场时偏向角的正切,由数学知识求解OP之长.
解答:解:(1)粒子进入金属板间做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,则得:
水平方向:L=v0t
竖直方向:y=
at2,a=
联立解得:y=
,即粒子偏离金属板时侧位移 OM=y=
.
(2)粒子飞出电场时竖直分速度 vy=at=
速度为 v=
=
.
(3)设粒子飞出电场时速度的偏向角为θ,则 tanθ=
=
根据数学知识得:OP=y+stanθ=
+
=
(
+s)
答:(1)粒子偏离金属板时侧位移OM是
.(2)粒子飞出电场时的速度
.(3)OP之长为
(
+s).
水平方向:L=v0t
竖直方向:y=
| 1 |
| 2 |
| qU |
| md |
联立解得:y=
| qUL2 | ||
2md
|
| qUL2 | ||
2md
|
(2)粒子飞出电场时竖直分速度 vy=at=
| qUL |
| mdv0 |
速度为 v=
|
|
(3)设粒子飞出电场时速度的偏向角为θ,则 tanθ=
| vy |
| v0 |
| qUL | ||
md
|
根据数学知识得:OP=y+stanθ=
| qUL2 | ||
2md
|
| qULs | ||
md
|
| qUL | ||
md
|
| L |
| 2 |
答:(1)粒子偏离金属板时侧位移OM是
| qUL2 | ||
2md
|
|
| qUL | ||
md
|
| L |
| 2 |
点评:带电粒子在匀强电场中的运动是考试的热点,关键是做好受力分析,明确粒子的运动情景,然后运用分解的观点或动能定理等逐步求解.

练习册系列答案
相关题目

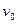 ,从两板中间射入,如图所示,已知电子质量为m,电量为e ,求:(电子的重力不计)
,从两板中间射入,如图所示,已知电子质量为m,电量为e ,求:(电子的重力不计)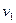 是多少?
是多少?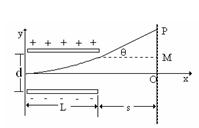
 ,从两板中间射入,如图所示,已知电子质量为m,电量为e ,求:(电子的重力不计)
,从两板中间射入,如图所示,已知电子质量为m,电量为e ,求:(电子的重力不计)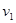 是多少?
是多少?