题目内容
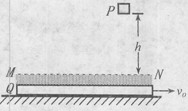
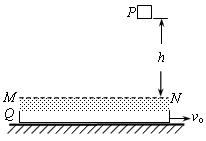
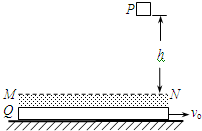 如图所示,P为质量为m=1kg的物块,Q为位于水平地面上的质量为M=4kg的特殊平板,平板与地面间的动摩因数μ=0.02.在板上表面的上方,存在一定厚度的“相互作用区域”,区域的上边界为MN.P刚从距高h=5m处由静止开始自由落下时,板Q向右运动的速度为vo=4m/s.当物块P进入相互作用区域时,P、Q之间有相互作用的恒力F=kmg,其中Q对P的作用竖直向上,k=21,F对P的作用使P刚好不与Q的上表面接触.在水平方向上,P、Q之间没有相互作用力,板Q足够长,空气阻力不计.( 取g=10m/s2,以下计算结果均保留两位有效数字)求:
如图所示,P为质量为m=1kg的物块,Q为位于水平地面上的质量为M=4kg的特殊平板,平板与地面间的动摩因数μ=0.02.在板上表面的上方,存在一定厚度的“相互作用区域”,区域的上边界为MN.P刚从距高h=5m处由静止开始自由落下时,板Q向右运动的速度为vo=4m/s.当物块P进入相互作用区域时,P、Q之间有相互作用的恒力F=kmg,其中Q对P的作用竖直向上,k=21,F对P的作用使P刚好不与Q的上表面接触.在水平方向上,P、Q之间没有相互作用力,板Q足够长,空气阻力不计.( 取g=10m/s2,以下计算结果均保留两位有效数字)求:(1)P第1次落到MN边界的时间t和第一次在相互作用区域中运动的时间T;
(2)P第2次经过MN边界时板Q的速度v;
(3)从P第1次经过MN边界到第2次经过MN边界的过程中,P、Q组成系统损失的机械能△E;
(4)当板Q速度为零时,P一共回到出发点几次?
分析:(1)物块P在到达MN边界前做自由落体运动,在相互作用区域先减速运动,然后反向加速运动,因此根据运动学规律可正确求解.
(2)注意当物块P到达相互作用区域时,Q对地面的压力增大,因此摩擦力发生变化,其运动的加速度也发生变化,理清其加速度的变化情况,然后根据运动规律求解.
(3)根据功能关系可以求出P、Q组成系统损失的机械能△E.
(4)物块P进入相互作用区域和离开时加速度不同,而且具有周期性,然后根据速度与时间的关系求解即可.
(2)注意当物块P到达相互作用区域时,Q对地面的压力增大,因此摩擦力发生变化,其运动的加速度也发生变化,理清其加速度的变化情况,然后根据运动规律求解.
(3)根据功能关系可以求出P、Q组成系统损失的机械能△E.
(4)物块P进入相互作用区域和离开时加速度不同,而且具有周期性,然后根据速度与时间的关系求解即可.
解答:解:(1)P自由落下第一次到达边界MN时:
h=
gt2,
所以:t=
=1s
P到达边界MN时速度:vP=
=10m/s
P进入相互作用区域时,kmg-mg=ma,a=(k-1)g=200m/s2
P第一次进入相互作用区域减速到零后又向上加速,以vP速度大小再次越过MN,所以运动时:
T=
=0.1s
故P第1次落到MN边界的时间t=1s,第一次在相互作用区域中运动的时间T=0.1s.
(2)上面分析知P先自由下落,以vP进入相互作用区域,减速到零后又向上加速,以vP速度大小再次越过MN,然后做竖直上抛运动回到原出发点,接着又重复上述运动过程.
每当P从出发点运动到MN的时间t内,板Q加速度a1向左,根据牛顿第二定律得:
a1=
=μg=0..2m/s2
每当P在相互作用区中运动的时间T内,板Q加速度a2向左,根据牛顿第二定律得:
a2=
=1.25m/s2
P第2次经过MN边界时,板Q的速度:
v=v0-a1t-a2T=3.7m/s
故P第2次经过MN边界时板Q的速度v=3.7m/s.
(3)P第1次经过MN边界时,板Q的速度:
v1=v0-a1t=3.8m/s
△E=
M
-
Mv2=15J
故P、Q组成系统损失的机械能△E=15J.
(4)设板Q速度为零时,P一共回到出发点n次.由以上分析得:
v0-2na1t-na2T=0
代入数据,解得n=7.6,故n取7
故当板Q速度为零时,P一共回到出发点7次.
h=
| 1 |
| 2 |
所以:t=
|
P到达边界MN时速度:vP=
| 2gh |
P进入相互作用区域时,kmg-mg=ma,a=(k-1)g=200m/s2
P第一次进入相互作用区域减速到零后又向上加速,以vP速度大小再次越过MN,所以运动时:
T=
| 2vP |
| a |
故P第1次落到MN边界的时间t=1s,第一次在相互作用区域中运动的时间T=0.1s.
(2)上面分析知P先自由下落,以vP进入相互作用区域,减速到零后又向上加速,以vP速度大小再次越过MN,然后做竖直上抛运动回到原出发点,接着又重复上述运动过程.
每当P从出发点运动到MN的时间t内,板Q加速度a1向左,根据牛顿第二定律得:
a1=
| μMg |
| M |
每当P在相互作用区中运动的时间T内,板Q加速度a2向左,根据牛顿第二定律得:
a2=
| μ(kmg+Mg) |
| M |
P第2次经过MN边界时,板Q的速度:
v=v0-a1t-a2T=3.7m/s
故P第2次经过MN边界时板Q的速度v=3.7m/s.
(3)P第1次经过MN边界时,板Q的速度:
v1=v0-a1t=3.8m/s
△E=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
故P、Q组成系统损失的机械能△E=15J.
(4)设板Q速度为零时,P一共回到出发点n次.由以上分析得:
v0-2na1t-na2T=0
代入数据,解得n=7.6,故n取7
故当板Q速度为零时,P一共回到出发点7次.
点评:本题的难点是对Q正确进行受力分析,弄清楚其加速度的变化,从而明确运动规律,然后根据运动学规律或者功能关系求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2006?佛山模拟)如图所示,P为一倾角α=37°的斜面.物体A质量为M,置于斜面上时其上表面水平,与斜面间动摩擦因数μ=0.25.物体B质量为m,当置于A上时与A间的摩擦力足够大.(取sin37°=0.6,cos37°=0.8,g=10m/s2.)试求:
(2006?佛山模拟)如图所示,P为一倾角α=37°的斜面.物体A质量为M,置于斜面上时其上表面水平,与斜面间动摩擦因数μ=0.25.物体B质量为m,当置于A上时与A间的摩擦力足够大.(取sin37°=0.6,cos37°=0.8,g=10m/s2.)试求: