题目内容
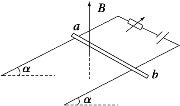
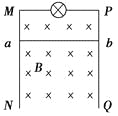
【题目】如图所示,MN和PQ为竖直方向的两平行长直金属导轨,间距L为1m,电阻不计。导轨所在的平面与磁感应强度B为1T的匀强磁场垂直。质量m=0.2 kg、电阻r=1Ω的金属杆ab始终垂直于导轨并与其保持光滑接触,导轨的上端有阻值为R=3Ω的灯泡。金属杆从静止下落,当下落高度为h=4m后灯泡保持正常发光。重力加速度为g=10m/s2。求:
(1)灯泡的额定功率;
(2)金属杆从静止下落4m的过程中通过灯泡的电荷量;
(3)金属杆从静止下落4m的过程中灯泡所消耗的电能.
【答案】(1)12 W(2)1 C(3)1.2 J
【解析】试题(1)灯泡保持正常发光时,金属杆做匀速运动,重力与安培力二力平衡,列出平衡方程,可得到灯泡的额定电流,即可求得其额定功率.
(2)根据法拉第电磁感应定律、欧姆定律和电量的公式结合求解电量.
(3)根据能量守恒定律求解灯泡所消耗的电能.
解:(1)灯泡保持正常发光时,金属杆做匀速运动 mg=BIL
得灯泡正常发光时的电流 I=![]() =
=![]() A=2A
A=2A
则额定功率P=I2R=22×3W="12" W
(2)平均电动势![]() =
=![]() ,平均电流
,平均电流![]() =
=![]()
则电荷量q=![]() △t=
△t=![]() =
=![]() C="1" C
C="1" C
(3)E=I(R+r)=BLv
得金属杆匀速时的速度为v=![]() =
=![]() ="8" m/s
="8" m/s
由能量守恒有:mgh=![]() mv2+W电
mv2+W电
得回路中消耗的总的电能W电="1.6" J
则灯泡所消耗的电能WR=![]() W电=
W电=![]() ×1.6J="1.2" J
×1.6J="1.2" J
答:
(1)灯泡的额定功率是12W;
(2)金属杆从静止下落4m的过程中通过灯泡的电荷量是1C;
(3)金属杆从静止下落4m的过程中灯泡所消耗的电能是1.2J.

练习册系列答案
相关题目