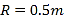Question

【题目】如图，半径为R=1m,内径很小的光滑半圆管竖直放置，左端接有两段光滑直轨道，AB与圆管外壁相切，BC与AB通过一段极短的圆弧平滑相连且BC倾角θ=45°。一个直径略小于半圆管内径、质量为m=lkg的小球，从BC轨道上与圆管圆心O等高的P点以某一速度沿轨道下滑，经圆管最高点D后恰好落回到P点。若小球经过D点时恰好与圆管没有相互作用，空气阻力忽略不计，重力加速度为g,求：

(1)水平轨道AB的长度；

(2)小球从P点滑到B点的时间；

(3)若改变小球从P点下滑的初始速度，小球从D点抛出落回到BC轨道时的动能也随之改变，求小球落到BC轨道时动能的最小值。

Answer 1

【答案】(1) (2) (3)

【解析】（1）物体过D点时，有：

D到P做平抛运动，有水平位移

竖直位移

又AB间距

解得：

(2)对小球，P到D由机械能守恒，有：

P到B做匀加速直线运动，

其中，，

解得P到B的时间

(3)假设小球过D点的速度为v，从D点落回BC下落的高度为h()

则小球落到BC时动能

其中，

又有几何关系

联立得：

当，即时，动能最小.