题目内容
【题目】如图所示，在质量为m＝1 kg的重物上系着一条长30 cm的细绳，细绳的另一端连着一个轻质圆环，圆环套在水平的棒上可以滑动，环与棒间的动摩擦因数μ为0.75，另有一条细绳，在其一端跨过定滑轮，定滑轮固定在距离圆环50 cm的地方，当细绳的另一端挂上重物G，而圆环将要开始滑动，（设最大静摩擦力等于滑动摩擦力，sin 37°＝0.6，g取10 m/s2）求：
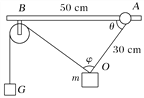
（1）角φ；
（2）长为30 cm的细绳的拉力T；
（3）圆环将要开始滑动时，重物G的质量。
【答案】（1）
（2）FT=8N（3）
【解析】（1）因为圆环将要开始滑动，所以，可以判定本题是在共点力作用下重物的平衡问题，对环进行受力分析：
······················· （1分）
······················· （1分）
解得
······················ （1分）
θ=53度，又由于AO=30cm， AB=50cm，即得······· （2分）
（2）如图所示选取坐标轴，根据物体m处于平衡状态，则有：
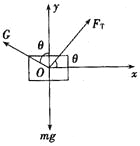
·················· （1分）
····················· （1分）
解得FT="8N··························" （2分）
（3）圆环将要滑动时，对重物进行受力分析可知：
······················ （1分）
又
························· （1分）
解得······················· （1分）
当圆环刚开始滑动时，绳子的拉力在水平方向的分力刚好等于最大静摩擦力，以圆环为研究对象画出受力分析图列平衡式求得角度θ，由绳子长度和几何关系可解，求绳子拉力时分别以物体m、G为研究对象，分析受力情况，建立直角坐标系，列方程求解
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
