Question

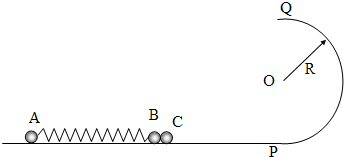
质量为m的小球，分别用长为L的细杆和细绳各自悬于固定点，且可绕固定点自由转动，要使小球刚好在竖直面内完成圆周运动，则两种情况小球在最低点的速度之比（　　）

• A．1：1
• B．1：2
• C．

  4

  ：

  5

• D．4：5

Answer 1

分析：小球恰好能通过最高点完成完整的圆周运动，知在最高点靠重力提供向心力，根据牛顿第二定律求出小球过b点时的速度．根据机械能守恒定律求出小球初速度的大小．
根据小球在最高点的拉力，结合牛顿第二定律求出小球经过最高点的速度大小．根据机械能守恒定律求出小球经过最低点时的速度大小．

解答：解：小球在杆的作用下，在最高点，支持力F=mg
根据牛顿第二定律得，F-mg=m

v 2 1

L

解得v₁=0．
根据机械能守恒定律得，mg?2L=

1

2

m

v

2 2

代入数据解得，v₂=

4gL

．
小球在绳子作用下，小球在最高点：mg=m

v 2 b

L

解得：v_b=

gL

从a点到最高点b的过程中，由机械能转化和守恒定律得：

1

2

mv₀²=2mgL+

1

2

mv_b²
解得：v₀=

5gL

因此两种情况小球在最低点的速度之比为

4

：

5

，故C正确，ABD错误；
故选C

点评：本题考查牛顿第二定律和机械能守恒定律的综合，知道圆周运动向心力的来源，结合牛顿第二定律进行求解．