题目内容
(2010?宁河县一模)如图所示,光滑轨道的DP段为水平轨道,PQ段为半径是R的竖直半圆轨道,半圆轨道的下端与水平的轨道的右端相切于P点.一轻质弹簧两端分别固定质量为2m的小球A和质量为m的小球B,质量为m小球C靠在B球的右侧.现用外力作用在A和C上,弹簧被压缩(弹簧仍在弹性限度内).这时三个小球均静止于距离P端足够远的水平轨道上.若撤去外力,C球恰好可运动到轨道的最高点Q.已知重力加速度为g.求撤去外力前的瞬间,弹簧的弹性势能E是多少?
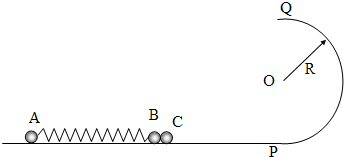

分析:C球恰好可运动到轨道的最高点Q,根据牛顿第二定律求出在C点速度.
对A、B、C及弹簧组成的系统,由动量守恒定律和能量守恒列出等式求解
对A、B、C及弹簧组成的系统,由动量守恒定律和能量守恒列出等式求解
解答:解:对A、B、C及弹簧组成的系统,当弹簧第一次恢复原长时,设B、C共同速度大小为υ0,A的速度大小为υA,由动量守恒定律有
2mυA=(m+m) υ0①
则υA=υ0
由系统能量守恒有E=
2mυA2+
(m+m)υ02②
此后B、C分离,设C恰好运动至最高点Q的速度为υ,此过程C球机械能守恒,则
mg?2R=
mυ02-
mυ2③
在最高点Q,由牛顿第二定律得mg=
④
联立①-----④式解得:E=10mgR
答:撤去外力前的瞬间,弹簧的弹性势能E是10mgR
2mυA=(m+m) υ0①
则υA=υ0
由系统能量守恒有E=
| 1 |
| 2 |
| 1 |
| 2 |
此后B、C分离,设C恰好运动至最高点Q的速度为υ,此过程C球机械能守恒,则
mg?2R=
| 1 |
| 2 |
| 1 |
| 2 |
在最高点Q,由牛顿第二定律得mg=
| mv2 |
| R |
联立①-----④式解得:E=10mgR
答:撤去外力前的瞬间,弹簧的弹性势能E是10mgR
点评:本题考查了能量的转化和守恒,同时还有机械能守恒和牛顿第二定律,涉及的知识点较多,对学生的能力要求较高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010?宁河县一模)如图所示为一理想变压器,原、副线圈的匝数比为n.原线圈接电压为u=U0sinωt的正弦交流电,输出端接有一个交流电流表和一个电动机,电动机的线圈电阻为R.当输入端接通电源后,电动机带动一质量为m的重物匀速上升,此时电流表的示数为I,重力加速度为g,下列说法正确的是( )
(2010?宁河县一模)如图所示为一理想变压器,原、副线圈的匝数比为n.原线圈接电压为u=U0sinωt的正弦交流电,输出端接有一个交流电流表和一个电动机,电动机的线圈电阻为R.当输入端接通电源后,电动机带动一质量为m的重物匀速上升,此时电流表的示数为I,重力加速度为g,下列说法正确的是( ) (2010?宁河县一模)如图所示,在x轴上方的空间存在着垂直于纸面向里的匀强磁场,磁感应强度的大小为B.许多相同的离子,以相同的速率v,由O点沿纸面向各个方向(y>0)射入磁场区域.不计离子所受重力,不计离子间的相互影响.图中曲线表示离子运动的区域边界,其中边界与y轴交点为M,边界与x轴交点为N,且OM=ON=L.由此可判断( )
(2010?宁河县一模)如图所示,在x轴上方的空间存在着垂直于纸面向里的匀强磁场,磁感应强度的大小为B.许多相同的离子,以相同的速率v,由O点沿纸面向各个方向(y>0)射入磁场区域.不计离子所受重力,不计离子间的相互影响.图中曲线表示离子运动的区域边界,其中边界与y轴交点为M,边界与x轴交点为N,且OM=ON=L.由此可判断( ) (2010?宁河县一模)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )
(2010?宁河县一模)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )