题目内容
18.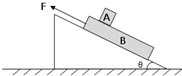 如图所示,一质量为M的斜面体静止在水平地面上,物体B受沿斜面向上力F作用沿斜面匀速上滑,A、B之间动摩擦因数为μ,μ<tanθ,且A、B质量均为m,则( )
如图所示,一质量为M的斜面体静止在水平地面上,物体B受沿斜面向上力F作用沿斜面匀速上滑,A、B之间动摩擦因数为μ,μ<tanθ,且A、B质量均为m,则( )| A. | A、B保持相对静止 | |
| B. | B与斜面间动摩擦因数为$\frac{F-mgsinθ-μmgcosθ}{2mgcosθ}$ | |
| C. | 地面对斜面体的摩擦力等于mg(sinθ-μcosθ)cosθ+Fcosθ | |
| D. | 地面受到的压力等于(M+2m)g-Fsinθ-mg(sinθ-μcosθ)sinθ |
分析 对A物体受力分析,根据力的合成与分解可以分析A受力的情况.再对A、B和斜面体组成的整体受力分析可得出斜面体的支持力的情况,从而得到斜面体对地面的压力.
解答 解:A、对A分析,因为μ<tanθ,则mgsinθ>μmgcosθ,则A、B不能保持相对静止,故A错误.
B、B对斜面体的正压力N=2mgcosθ,对B分析,根据共点力平衡有:F=mgsinθ+μmgcosθ+f′,
则B与斜面间动摩擦因数 μ′=$\frac{f′}{N}$=$\frac{F-mgsinθ-μmgcosθ}{2mgcosθ}$.故B正确.
CD、以A为研究的对象,A受到重力、支持力和斜面体B对A的摩擦力,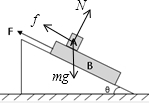 垂直于斜面的方向:N=mgcosθ
垂直于斜面的方向:N=mgcosθ
沿斜面的方向:mgsinθ-μN=maA
由于μ<tanθ,则:maA=mgsinθ-μmgcosθ>0
加速度 aA=gsinθ-μgcosθ,
将A、B和斜面体视为整体,受力分析
根据牛顿第二定律得:
将加速度分解,可得水平方向有:f-Fcosθ=maAcosθ,解得:地面对斜面体的摩擦力 f=mg(sinθ-μcosθ)cosθ+Fcosθ
竖直方向有:(M+2m)g-Fsinθ-FN=maAsinθ,得 FN=(M+2m)g-Fsinθ-m(gsinθ-μgcosθ)sinθ,
则由牛顿第三定律知:地面受到的压力为(M+2m)g-Fsinθ-m(gsinθ-μgcosθ)sinθ,故CD正确.
故选:BCD.
点评 解决本题时,由于B与斜面体之间的相互作用力不容易求出,但是,当以A、B与斜面体组成的整体为研究对象时,将加速度的分解即可完成.要灵活选取研究对象.

练习册系列答案
相关题目
6.如图所示,实线和虚线分别表示某电场的电场线和等势线,下列说法中正确的是( )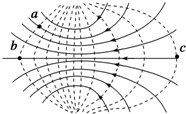

| A. | c点场强大于a点场强 | |
| B. | c点电势低于a点电势 | |
| C. | c、b两点间的电势差等于c、a两点间的电势差 | |
| D. | 若将一试探电荷+q由a点移动到b点,电场力做正功 |
7.在光电效应实验中,两个实验小组分别在各自的实验室,约定用相同频率的单色光,分别照射锌和银的表面,结果都能发生光电效应,如图甲,并记录相关数据.对于这两组实验,下列判断正确的是( )
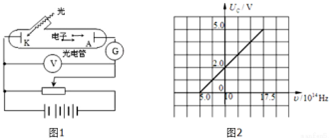

| A. | 饱和光电流一定不同 | |
| B. | 因为材料不同逸出功不同,所以遏止电压Uc不同 | |
| C. | 光电子的最大初动能不同 | |
| D. | 因为光强不确定,所以单位时间逸出的光电子数可能相同 | |
| E. | 分别用不同频率的光照射之后绘制Uc~ν图象(ν为照射光频率,图乙为其中一小组绘制的图象),图象的斜率可能不同 |
8.上海世博会的主题是“城市,让生活更美好”.其中一个重要的领域和内容就是“绿色、环保、节能”,使城市与环境和谐,使世博园区成为生态城市、和谐城市的样板.为此,世博园内启用了大量环保公交车,尽量使世博园区内交通“零排放”、园区周边交通“低排放”.假设某环保车正以3m/s2的加速度做匀加速直线运动,那么( )
| A. | 每秒钟环保车的速度增加3m/s | |
| B. | 环保车的末速度一定比初速度大3m/s | |
| C. | 第3秒初的速度比第2秒末的速度大3m/s | |
| D. | 第3秒末的速度比第2秒初的速度大3m/s |
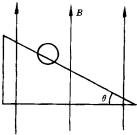 通电直导线沿水平方向放在倾角为θ的光滑斜面上,图中圆圈表示导线的横截面,匀强磁场的方向竖直向上,磁感应强变为B,导线在磁场中的长度为L.要使导线静止在斜面上,导线中的电流方向应该垂直纸面向外,若导线的质量为m,电流强度应是$\frac{mgtanθ}{BL}$.
通电直导线沿水平方向放在倾角为θ的光滑斜面上,图中圆圈表示导线的横截面,匀强磁场的方向竖直向上,磁感应强变为B,导线在磁场中的长度为L.要使导线静止在斜面上,导线中的电流方向应该垂直纸面向外,若导线的质量为m,电流强度应是$\frac{mgtanθ}{BL}$.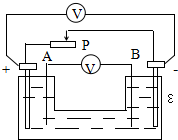 图示是研究闭合电路的内电压、外电压和电动势间关系装置:
图示是研究闭合电路的内电压、外电压和电动势间关系装置: 如图所示,R为电阻箱,V为理想电压表,当电阻箱读数为R1=2Ω时,电压表读数为U1=4V;当电阻箱读数为R2=5Ω时,电压表读数为U2=5V.求:
如图所示,R为电阻箱,V为理想电压表,当电阻箱读数为R1=2Ω时,电压表读数为U1=4V;当电阻箱读数为R2=5Ω时,电压表读数为U2=5V.求:
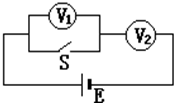 用两只电压表也可以测电源的电动势,如图所示.电压表V1与电键S并联,再串联电压表V2后与电源相连,当S断开时,V1的读数为12V,V2的读数为6V,当S闭和时V2的读数为15V.求该电源的电动势.
用两只电压表也可以测电源的电动势,如图所示.电压表V1与电键S并联,再串联电压表V2后与电源相连,当S断开时,V1的读数为12V,V2的读数为6V,当S闭和时V2的读数为15V.求该电源的电动势.