题目内容
17. 一质量为1600kg的汽车,行驶到一座半径为40m的圆弧形拱桥顶端时,汽车运动速度为10m/s,g=10m/s2.求:
一质量为1600kg的汽车,行驶到一座半径为40m的圆弧形拱桥顶端时,汽车运动速度为10m/s,g=10m/s2.求:(1)此时汽车的向心加速度大小;
(2)此时汽车对桥面压力的大小;
(3)若要汽车通过顶端时对桥面的压力为零,则汽车在顶端时的行驶速度应该为多大.
分析 根据汽车的速度大小,结合 向心加速度公式求出向心加速度大小.根据牛顿第二定律求出支持力的大小,从而得出汽车对桥面的压力大小.
当汽车对桥面的压力为零时,靠重力提供向心力,结合牛顿第二定律求出汽车在顶端时的速度大小.
解答 解:(1)汽车向心加速度大小为:a=$\frac{{v}^{2}}{r}$=$\frac{100}{40}m/{s}^{2}$=2.5m/s2
(2)支持力为FN,则有:mg-FN=ma,
代入数据解得:FN=12000N
由牛顿第三定律,压力为:FN′=12000N
(3)当压力为零时,根据mg=$m\frac{{{v}_{m}}^{2}}{R}$
解得:vm=$\sqrt{gR}=\sqrt{10×40}m/s$=20m/s.
答:(1)汽车的向心加速度大小为2.5m/s2;
(2)汽车对桥面的压力大小为12000N;
(3)汽车在顶端时的速度为20m/s.
点评 解决本题的关键知道汽车在顶端向心力的来源,结合牛顿第二定律进行求解,基础题.

练习册系列答案
相关题目
8.关于电场线的说法中正确的是( )
| A. | 电场中任何两条电场线都不相交 | |
| B. | 电场线上每一点的切线方向跟电荷在该点受电场力的方向相同 | |
| C. | 沿电场线方向场强越来越小 | |
| D. | 电场线越密集的地方同一检验电荷受电场力越大 |
12.下列不属于匀变速运动的是( )
| A. | 自由落体运动 | B. | 平抛运动 | C. | 斜上抛运动 | D. | 匀速圆周运动 |
6.下列说法正确的是( )
| A. | 两个互成角度的匀变速直线运动的合运动不可能是直线运动 | |
| B. | 做曲线运动的物体的合力一定是变化的 | |
| C. | 平抛运动的物体在相等的时间内速度变化量相同 | |
| D. | 做匀速圆周运动的物体的加速度是恒定不变的 |
7.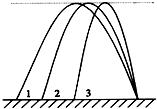 如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
 如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )| A. | 沿路径1抛出的物体落地的速率最大 | |
| B. | 沿路径3抛出的物体在空中运动的时间最长 | |
| C. | 三个物体抛出时初速度的竖直分量相等 | |
| D. | 三个物体抛出时初速度的水平分量相等 |
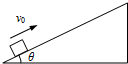 如图所示,质量m=0.1kg的木块沿倾角θ=30°的固定斜面从某一位置以v0=6.0m/s的初速度向上运动.已知木块与斜面间的动摩擦因数μ=$\frac{{\sqrt{3}}}{3}$,取木块初始位置为重力势能的参考平面,g=10m/s2,求:
如图所示,质量m=0.1kg的木块沿倾角θ=30°的固定斜面从某一位置以v0=6.0m/s的初速度向上运动.已知木块与斜面间的动摩擦因数μ=$\frac{{\sqrt{3}}}{3}$,取木块初始位置为重力势能的参考平面,g=10m/s2,求: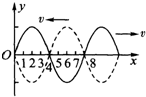 两列简谐波频率相等,波速大小相等,分别沿+x和-x传播,如图所示,图中x=1,2,3,4,5,6,7,8各点中振幅最大的是x=4和8的点,振幅最小的是x=2和6的点.
两列简谐波频率相等,波速大小相等,分别沿+x和-x传播,如图所示,图中x=1,2,3,4,5,6,7,8各点中振幅最大的是x=4和8的点,振幅最小的是x=2和6的点.