题目内容
2.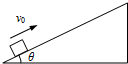 如图所示,质量m=0.1kg的木块沿倾角θ=30°的固定斜面从某一位置以v0=6.0m/s的初速度向上运动.已知木块与斜面间的动摩擦因数μ=$\frac{{\sqrt{3}}}{3}$,取木块初始位置为重力势能的参考平面,g=10m/s2,求:
如图所示,质量m=0.1kg的木块沿倾角θ=30°的固定斜面从某一位置以v0=6.0m/s的初速度向上运动.已知木块与斜面间的动摩擦因数μ=$\frac{{\sqrt{3}}}{3}$,取木块初始位置为重力势能的参考平面,g=10m/s2,求:(1)当木块的动能等于重力势能时,木块相对于初始位置的高度h.
(2)木块在上滑到最高点的过程中克服摩擦力做的功Wf.
分析 (1)由题设条件:木块的动能等于重力势能,列式;再由动能定理列式,联立可求高度h.
(2)先根据动能定理求出物体上升的最大高度,再由功的公式求克服摩擦力做的功Wf.
解答 解:(1)当木块动能与重力势能相等时,设木块的速度为v,由动能定理,有
$-mgh-μmgcosθ\frac{h}{sinθ}=\frac{1}{2}m{v^2}-\frac{1}{2}mv_0^2$
由题意,有 ${E_P}=mgh=\frac{1}{2}m{v^2}$
由以上两式,得:$h=\frac{v_0^2}{2g(2+μcotθ)}=\frac{6^2}{{2×10×(2+\frac{{\sqrt{3}}}{3}cot{{30}°})}}m=0.6m$
(2)取能上滑的最大高度为H,由动能定理,有
$-mgH-μmgcosθ\frac{H}{sinθ}=0-\frac{1}{2}mv_0^2$
解得:$H=\frac{v_0^2}{2g(1+μcotθ)}=\frac{6^2}{{2×10×(1+\frac{{\sqrt{3}}}{3}cot{{30}°})}}m=0.9m$
则 ${W_f}=μmgcos{30°}\frac{H}{{sin{{30}°}}}=0.9J$
答:
(1)当木块的动能等于重力势能时,木块相对于初始位置的高度h为0.6m.
(2)木块在上滑到最高点的过程中克服摩擦力做的功Wf为0.9J.
点评 涉及力在空间的效果时,要优先考虑动能定理,运用动能定理时要灵活选择研究的过程.动能定理还是求功常用的方法之一.

练习册系列答案
相关题目
12.两块电压表V1和V2是由完全相同的电流表改装成的.V2的量程为5V,V1的量程为15V,为了测量15V-20V的电压,把V1和V2串联起来使用,在这种情况下( )
| A. | V1和V2的读数相等 | |
| B. | V1和V2的指针偏转角度相等 | |
| C. | V1和V2的读数之比等于两个电压表内阻之比 | |
| D. | V1和V2指针偏转角之比等于两个电压表内阻之比 |
14.关于功和能的说法正确的是( )
| A. | 功是能量转化的量度 | B. | 功是矢量,能量是标量 | ||
| C. | 功和能的单位都是焦耳 | D. | 功和能都是状态量 |
11. 一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离.假定空气阻力可忽略,运动员可视为质点,从绳子绷紧到最低点的下落过程中,下列说法正确的是( )
一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离.假定空气阻力可忽略,运动员可视为质点,从绳子绷紧到最低点的下落过程中,下列说法正确的是( )
 一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离.假定空气阻力可忽略,运动员可视为质点,从绳子绷紧到最低点的下落过程中,下列说法正确的是( )
一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离.假定空气阻力可忽略,运动员可视为质点,从绳子绷紧到最低点的下落过程中,下列说法正确的是( )| A. | 运动员的动能不断增大 | |
| B. | 运动员克服弹力做功,弹性势能增加 | |
| C. | 运动员重力势能始终减小 | |
| D. | 重力势能的改变量与重力势能零点的选取有关 |
12.下列说法中正确的是( )
| A. | 玛丽•居里首先提出原子的核式结构学说 | |
| B. | 查德威克第一个发现中子 | |
| C. | 卢瑟福在“a粒子散射实验”中发现了电子 | |
| D. | 普朗克为解释光电效应的实验规律提出了光子说 |
 一质量为1600kg的汽车,行驶到一座半径为40m的圆弧形拱桥顶端时,汽车运动速度为10m/s,g=10m/s2.求:
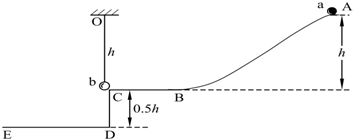
一质量为1600kg的汽车,行驶到一座半径为40m的圆弧形拱桥顶端时,汽车运动速度为10m/s,g=10m/s2.求: 如图所示,A、B两点中有一点是振源,相距1.2m,所产生的简谐横波沿直线传播.从振源开始振动时开始计时,已知在4s内,A质点完成了8次全振动,B质点完成了10次全振动,则该列波传播的方向是从B到A,波速为1.5m/s.
如图所示,A、B两点中有一点是振源,相距1.2m,所产生的简谐横波沿直线传播.从振源开始振动时开始计时,已知在4s内,A质点完成了8次全振动,B质点完成了10次全振动,则该列波传播的方向是从B到A,波速为1.5m/s.