题目内容
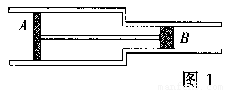
 如图,气缸由两个截面不同的圆筒连接而成,活塞A、B被轻质刚性细杆连接在一起,可无摩擦移动,A、B的质量分别mA=12kg,mB=8.0kg,SA=4.0×10-2m2,横截面积分别为SB=2.0×10-2m2,一定质量的理想气体被封闭在两活塞之间,活塞外侧与大气相通,大气p0=1.0×105Pa.
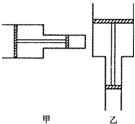
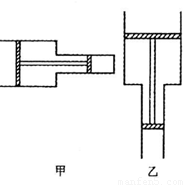
如图,气缸由两个截面不同的圆筒连接而成,活塞A、B被轻质刚性细杆连接在一起,可无摩擦移动,A、B的质量分别mA=12kg,mB=8.0kg,SA=4.0×10-2m2,横截面积分别为SB=2.0×10-2m2,一定质量的理想气体被封闭在两活塞之间,活塞外侧与大气相通,大气p0=1.0×105Pa.(l)气缸水平放置达到如图甲所示的平衡状态,求气体的压强.
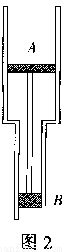
(2)已知此时气体的体积V1=2.0×10-2m3.现保持温度不变,将气缸竖直放置,达到平衡后如图乙所示.与图甲相比,活塞在气缸内移动的距离L为多少?取重力加速度g=10m/s2.
分析:(1)以活塞A、B及刚性细杆为研究对象,在水平方向上进行受力分析,列式可求出气体的压强.
(2)以活塞A、B及刚性细杆为研究对象,在竖直方向上放上受力分析,列式可求出气体的压强;
然后根据玻意耳定律列方程求出L.
(2)以活塞A、B及刚性细杆为研究对象,在竖直方向上放上受力分析,列式可求出气体的压强;
然后根据玻意耳定律列方程求出L.
解答:解:(1)气缸处于甲图所示位置时,设气缸内气体压强为P1,对于活塞和杆,
由力的平衡条件得:p0SA+p1SB+p1SA=p0SB
解得:p1=p0=1.0×105Pa
(2)汽缸处于乙图所示位置时,设气缸内气体压强为p2,对于活塞和杆,
由力的平衡条件得:p0SA+p2SB+(mA+mB)g=p2SA+p0SB
设V2为气缸处于乙图所示位置时缸内气体的体积,由玻意耳定律可得:p1V1=p2V2
由几何关系可得:V1-V2=L(SA-SB)
由上述各式解得活塞在气缸内移动距离:L=9.1×10-2m
答:(l)气缸水平放置达到如图甲所示的平衡状态,求气体的压强1.0×105Pa.
(2)气体的体积V1=2.0×10-2m3.现保持温度不变,将气缸竖直放置,达到平衡后如图乙所示.与图甲相比,活塞在气缸内移动的距离L为9.1×10-2m.
由力的平衡条件得:p0SA+p1SB+p1SA=p0SB
解得:p1=p0=1.0×105Pa
(2)汽缸处于乙图所示位置时,设气缸内气体压强为p2,对于活塞和杆,
由力的平衡条件得:p0SA+p2SB+(mA+mB)g=p2SA+p0SB
设V2为气缸处于乙图所示位置时缸内气体的体积,由玻意耳定律可得:p1V1=p2V2
由几何关系可得:V1-V2=L(SA-SB)
由上述各式解得活塞在气缸内移动距离:L=9.1×10-2m
答:(l)气缸水平放置达到如图甲所示的平衡状态,求气体的压强1.0×105Pa.
(2)气体的体积V1=2.0×10-2m3.现保持温度不变,将气缸竖直放置,达到平衡后如图乙所示.与图甲相比,活塞在气缸内移动的距离L为9.1×10-2m.
点评:该题是求解被封闭气体压强的题,往往是要先确定研究对象,对其受力分析,由平衡条件列式求解.在选取研究对象上,往往以受力较少的物体为研究对象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,气缸由两个横截面不同的圆筒连接而成.活塞A、B被轻刚性细杆连接在一起,可无摩擦移动.A、B的质量分别为mA=12kg,mB=8.0kg,横截面积分别为SA=4.0×10-2m2,SB=2.0×10-2m2.一定质量的理想气体被封闭在两活塞之间.活塞外侧大气压强P0=1.0×105Pa.
如图,气缸由两个横截面不同的圆筒连接而成.活塞A、B被轻刚性细杆连接在一起,可无摩擦移动.A、B的质量分别为mA=12kg,mB=8.0kg,横截面积分别为SA=4.0×10-2m2,SB=2.0×10-2m2.一定质量的理想气体被封闭在两活塞之间.活塞外侧大气压强P0=1.0×105Pa.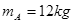 ,
,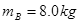 ,
,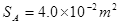 ,横截面积分别为
,横截面积分别为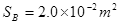 ,一定质量的理想气体被封闭在两活塞之间,活塞外侧与大气相通,大气
,一定质量的理想气体被封闭在两活塞之间,活塞外侧与大气相通,大气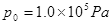 。
。
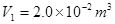 。现保持温度不变,将气缸竖直放置,达到平衡后如图乙所示。与图甲相比,活塞在气缸内移动的距离L为多少?取重力加速度
。现保持温度不变,将气缸竖直放置,达到平衡后如图乙所示。与图甲相比,活塞在气缸内移动的距离L为多少?取重力加速度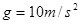 。
。