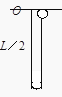题目内容
【题目】如图所示,光滑斜面的倾角α=30°,在斜面上放置一矩形线框abcd,ab边的边长![]() ,bc边的边长
,bc边的边长![]() ,线框的质量m=1kg,电阻R=0.1Ω,线框通过细线与重物相连,重物质量M=2kg,斜面上ef线(ef∥gh)的右方有垂直斜面向上的匀强磁场,磁感应强度B=0.5T,如果线框从静止开始运动,进入磁场最初一段时间是匀速的,ef线和gh的距离s=11.4m,(取
,线框的质量m=1kg,电阻R=0.1Ω,线框通过细线与重物相连,重物质量M=2kg,斜面上ef线(ef∥gh)的右方有垂直斜面向上的匀强磁场,磁感应强度B=0.5T,如果线框从静止开始运动,进入磁场最初一段时间是匀速的,ef线和gh的距离s=11.4m,(取![]() ),求:
),求:

(1)线框进入磁场前重物M的加速度;
(2)线框进入磁场时匀速运动的速度v;
(3)ab边由静止开始到运动到gh线处所用的时间t;
(4)ab边运动到gh线处的速度大小和在线框由静止开始到运动到gh线的整个过程中产生的焦耳热.
【答案】(1)a=5m/s2;(2)v=6m/s;(3)t=2.5s;(4)Q=9J
【解析】试题分析:(1)线框进入磁场前,线框仅受到细线的拉力![]() ,斜面的支持力和线框重力,重物M受到重力和拉力
,斜面的支持力和线框重力,重物M受到重力和拉力![]() .则由牛顿第二定律得:
.则由牛顿第二定律得:
对重物有: ![]()
对线框有: ![]() .
.
联立解得线框进入磁场前重物M的加速度为: ![]() 。
。
(2)因为线框进入磁场的最初一段时间做匀速运动,所以重物受力平衡![]() ,
,
线框![]() 受力平衡
受力平衡![]() ,
, ![]() 边进入磁场切割磁感线,产生的电动势为:
边进入磁场切割磁感线,产生的电动势为: ![]() ;形成的感应电流为:
;形成的感应电流为: ![]()
受到的安培力为: ![]()
联立上述各式得: ![]()
代入数据![]() ,解得:
,解得: ![]() 。
。
(3)线框![]() 进入磁场前时,做匀加速直线运动;进磁场的过程中,做匀速直线运动;进入磁场后到运动到
进入磁场前时,做匀加速直线运动;进磁场的过程中,做匀速直线运动;进入磁场后到运动到![]() 线,仍做匀加速直线运动.进磁场前线框的加速度大小与重物的加速度相同,为:
线,仍做匀加速直线运动.进磁场前线框的加速度大小与重物的加速度相同,为: ![]()
该阶段运动时间为: ![]()
进磁场过程中匀速运动时间为: ![]()
线框完全进入磁场后线框受力情况同进入磁场前,所以该阶段的加速度仍为: ![]() ,
, ![]() ;代入得:
;代入得: ![]()
解得: ![]() ,因此
,因此![]() 边由静止开始运动到
边由静止开始运动到![]() 线所用的时间为:
线所用的时间为: ![]() 。
。
(4)线框![]() 边运动到
边运动到![]() 处的速度为:
处的速度为: ![]() ,整个运动过程产生的焦耳热为:
,整个运动过程产生的焦耳热为: ![]() 。
。

 阅读快车系列答案
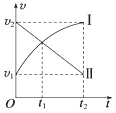
阅读快车系列答案【题目】要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道.求摩托车在直道上行驶所用的最短时间,有关数据见表格.某同学是这样解的:要使摩托车所用时间最短,应先由静止加速到最大速度v1=40m/s,然后再减速到v2=20m/s,t1= ![]() =…;t2=
=…;t2= ![]() =…;t=t1+t2=…
=…;t=t1+t2=…
你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果.
启动加速度a1 | 4m/s2 |
制动加速度a2 | 8m/s2 |
直道最大速度v1 | 40m/s |
弯道最大速度v2 | 20m/s |
直道长度x | 167m |