题目内容
11. 如图所示,质量为m,半径为r的小球,放在内半径为R,质量为3m的大空心球内,大球开始静止在光滑水平面上,当小球由图中位置无初速释放沿内壁滚到最低点时,求大球移动的距离.
如图所示,质量为m,半径为r的小球,放在内半径为R,质量为3m的大空心球内,大球开始静止在光滑水平面上,当小球由图中位置无初速释放沿内壁滚到最低点时,求大球移动的距离.
分析 小球无初速下滑到达最低点时,小球与大球组成的系统水平方向动量守恒,用位移表示平均速度,根据水平方向平均动量守恒定律求出小球发生的水平位移,再由几何知识求出大球的位移.
解答 解:设小球滑到最低点所用的时间为t,发生的水平位移大小为R-r-x,大球的位移大小为x,取水平向左方向为正方向.则根据水平方向平均动量守恒得: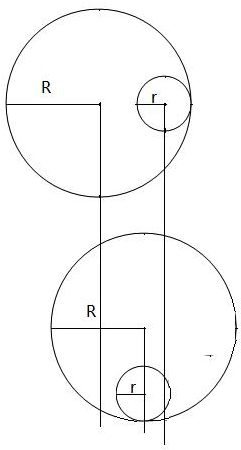
m$\overline{{v}_{1}}$-3m$\overline{{v}_{2}}$=0
即:m$\frac{R-r-x}{t}$=3m$\frac{x}{t}$
解得:x=$\frac{R-r}{4}$
答:大球移动的距离为$\frac{R-r}{4}$
点评 本题不能静止地看问题,把圆环当作不动的,要注意位移的参考系,注意运动过程中,水平方向动量守恒,中等难度.

练习册系列答案
相关题目
2.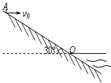 如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )
如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )
 如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )
如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )| A. | 若石块不能落入水中,则v0越大,落到斜面上时速度方向与斜面的夹角越大 | |
| B. | 若石块不能落入水中,则v0越大,落到斜面上时速度方向与斜面的夹角越小 | |
| C. | 若石块能落入水中,则v0越大,落水时速度方向与水平面的夹角越大 | |
| D. | 若v0=18m/s,则石块可以落入水中 |
19.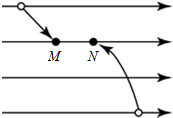 如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )
如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )
 如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )
如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )| A. | M的带电量比N的大 | B. | M带负电荷,N带正电荷 | ||
| C. | 静止时M受到的合力比N的大 | D. | 移动过程中匀强电场对M做负功 |
6. 把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )
把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )
 把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )
把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )| A. | A端的电势比B端的电势高 | |
| B. | A端的电荷比B端的电荷密集 | |
| C. | A端额电势可能比B端的电势高,也可能比B端的电势低 | |
| D. | A端的电势与B端的电势相等 |
3.在伽利略的斜面实验中,如果空气阻力和摩擦阻力不能忽略不计,则下列说法正确的是( )
| A. | 动能和势能之和仍守恒 | |
| B. | 动能和势能之和将增大 | |
| C. | 动能和势能之和将逐渐减小,但总的能量还是守恒的 | |
| D. | 以上说法均不对 |
20.对下列几种固体物质的认识,正确的有( )
| A. | 食盐熔化过程中,温度保持不变,说明食盐是晶体 | |
| B. | 烧热的针尖接触涂有蜂蜡薄层的云母片背面,熔化的蜂蜡呈椭圆形,说明蜂蜡是晶体 | |
| C. | 天然石英表现为各向异性,是由于该物质的微粒在空间的排列不规则 | |
| D. | 石墨和金刚石的物理性质不同,是由于组成它们的物质微粒排列结构不同 |
2. 图示的木箱a用细线悬挂在天花板下,木箱内有用竖直弹簧相连的两物块b和c,b放于木箱的水平地板上.已知木箱a的质量为m,物块b的质量为2m,物块c的质量为3m,起初整个装置静止不动.用符号g表示重力加速度,针对剪断细线的瞬间,下列判断正确的是( )
图示的木箱a用细线悬挂在天花板下,木箱内有用竖直弹簧相连的两物块b和c,b放于木箱的水平地板上.已知木箱a的质量为m,物块b的质量为2m,物块c的质量为3m,起初整个装置静止不动.用符号g表示重力加速度,针对剪断细线的瞬间,下列判断正确的是( )
 图示的木箱a用细线悬挂在天花板下,木箱内有用竖直弹簧相连的两物块b和c,b放于木箱的水平地板上.已知木箱a的质量为m,物块b的质量为2m,物块c的质量为3m,起初整个装置静止不动.用符号g表示重力加速度,针对剪断细线的瞬间,下列判断正确的是( )
图示的木箱a用细线悬挂在天花板下,木箱内有用竖直弹簧相连的两物块b和c,b放于木箱的水平地板上.已知木箱a的质量为m,物块b的质量为2m,物块c的质量为3m,起初整个装置静止不动.用符号g表示重力加速度,针对剪断细线的瞬间,下列判断正确的是( )| A. | 物块b下落的加速度为g | B. | 木箱a下落的加速度为2g | ||
| C. | 物块b对木箱底板的压力为mg | D. | 物块b对木箱底板的压力为2mg |
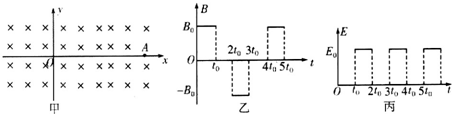
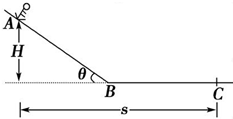 滑雪者从高为H的山坡上A点由静止下滑,到B点后又在水平雪面上滑行,最后停止在C点.A、C两点的水平距离为s,求滑雪板与雪面间的动摩擦因数μ.
滑雪者从高为H的山坡上A点由静止下滑,到B点后又在水平雪面上滑行,最后停止在C点.A、C两点的水平距离为s,求滑雪板与雪面间的动摩擦因数μ.