题目内容
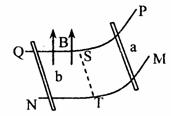
如图所示是两对接的轨道，两轨道与水平面的夹角均为α=30°，左轨道光滑，右轨道粗糙．一质点自左轨道上距O点L0处从静止起滑下，当质点第一次返回到左轨道并达到最高点时，它离O点的距离为
，两轨道对接处有一个很小的光滑圆弧，质点与轨道不会发生碰撞，求质点与右轨道的动摩擦因数．
| L0 |
| 3 |
设质点在右轨道上滑距离为L
根据动能定理，得
从左向右过程：mg（L0-L）sinα-μmgcosα?L=0 ①
从右向左过程：mg（L-
）sinα-μmgcos?L=0 ②
由①-②得
L=
L0
代入①解得μ=
答：质点与右轨道的动摩擦因数为
．
根据动能定理，得
从左向右过程：mg（L0-L）sinα-μmgcosα?L=0 ①
从右向左过程：mg（L-
| L0 |
| 3 |
由①-②得
L=
| 2 |
| 3 |
代入①解得μ=
| ||
| 6 |
答：质点与右轨道的动摩擦因数为
| ||
| 6 |
练习册系列答案
相关题目
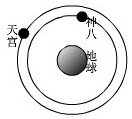
2012年6月18日，载有三名航天员的神舟九号飞船于下午14时许与天宫一号自动交会对接．对接完成、两飞行器形成稳定运行的组合体后，航天员于17时多进入天宫一号目标飞行器，这实现了中国载人航天历史上首次对一个在轨运行的航天器的拜访和驻留．假如神舟九号与天宫一号对接前所处的轨道如图所示，当它们处于如图所示的轨道运行时，下列说法正确的是（ ）
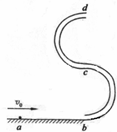如图所示的“s”形玩具轨道，该轨道是用内壁光滑的薄壁细圆管弯成，放置在竖直平面内，轨道弯曲部分是由两个半径相等的半圆对接而成，圆半径比细管内径大得多，轨网道底端与水平地面相切，轨道在水平方向不可移动．弹射装置将一个小球（小球的直径略小于细圆管内径）从a点沿水平地面向b点运动并进入轨道，经过轨道后从最高点d水平抛出．已知小球与地面ab段间的动摩擦因数为μ，ab段长L，圆的半径R，小球质量m，求：
,a棒从斜轨上高为0.50m处无初速释放，而b棒始终被拴接在距ST线1m处不动。求：
