题目内容
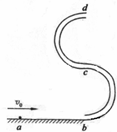 如图所示的“s”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,放置在竖直平面内,轨道弯曲部分是由两个半径相等的半圆对接而成,圆半径比细管内径大得多,轨网道底端与水平地面相切,轨道在水平方向不可移动.弹射装置将一个小球(小球的直径略小于细圆管内径)从a点沿水平地面向b点运动并进入轨道,经过轨道后从最高点d水平抛出.已知小球与地面ab段间的动摩擦因数为μ,ab段长L,圆的半径R,小球质量m,求:
如图所示的“s”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,放置在竖直平面内,轨道弯曲部分是由两个半径相等的半圆对接而成,圆半径比细管内径大得多,轨网道底端与水平地面相切,轨道在水平方向不可移动.弹射装置将一个小球(小球的直径略小于细圆管内径)从a点沿水平地面向b点运动并进入轨道,经过轨道后从最高点d水平抛出.已知小球与地面ab段间的动摩擦因数为μ,ab段长L,圆的半径R,小球质量m,求:(1)若小球经d处时,对轨道上臂有压力,则它经过b处时的速度满足什么条件?
(2)为使小球离开轨道d处后,不会再碰到轨道,则小球离开d出时的速度至少为多大?
(3)若μ=0.2、L=1m、R=0.2m、m=0.1kg,g取10m/s2,小球从a点出发的速度为4m/s,则它经c点前、后的瞬间,小球对轨道的压力各为多大?
分析:(1)根据牛顿第二定律与机械能守恒定律,即可求解;
(2)根据平抛运动规律处理的方法,运用牛顿第二定律与运动学公式综合,借助于几何关系,即可求解;
(3)根据动能定理,与牛顿第二定律,结合向心力表达式,即可求解.
(2)根据平抛运动规律处理的方法,运用牛顿第二定律与运动学公式综合,借助于几何关系,即可求解;
(3)根据动能定理,与牛顿第二定律,结合向心力表达式,即可求解.
解答: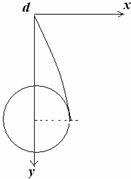 解:(1)根据牛顿第二定律,小球经d点时Fd+mg=m
解:(1)根据牛顿第二定律,小球经d点时Fd+mg=m
Fd>0,即vd>
小球从b到d,由机械能守恒定律
m
+4mgR=
m
解得vb>3
(2)假设恰好落到竖直位移3R处,则该点的速度方向竖直向下,这不符合平抛运动的规律.设小球离开d出时的速度为vd时,在运动过程中与轨道恰好相碰,即小球的运动轨迹与圆相切.以d点为坐标原点建立如图10坐标系,由平抛运动规律得
x=vdt①
y=
gt2②
由①②两式得y=
x2③
由解析几何知识得x2+(y-3R)2=R2④
联立③④两式得y2+(
-6R)y+8R2=0⑤
要使的抛物线与圆相切,则方程⑤的△判别式为零,即△=(
-6R)2-32R2=0
解得:vd=
故小球离开轨道d处后,不再碰到轨道,小球离开d出时的速度至少为
(3)小球从a到c,由动能定理得:
-μmgL-2mgR=
m
-
m
解得vc=2m/s
由牛顿第二定律得
小球在c点前,F1+mg=m
解得F1=1N,(方向竖直向下)
小球在c点后,F2-mg=m
解得F2=3N,(方向竖直向上)
答:(1)若小球经d处时,对轨道上臂有压力,则它经过b处时的速度满足vb>3
条件;
(2)为使小球离开轨道d处后,不会再碰到轨道,则小球离开d出时的速度至少为
;
(3)则小球对轨道的压力各为F1=1N,(方向竖直向下);F2=3N,(方向竖直向上).
 解:(1)根据牛顿第二定律,小球经d点时Fd+mg=m
解:(1)根据牛顿第二定律,小球经d点时Fd+mg=m
| ||
| R |
Fd>0,即vd>
| gR |
小球从b到d,由机械能守恒定律
| 1 |
| 2 |
| v | 2 d |
| 1 |
| 2 |
| v | 2 b |
解得vb>3
| gR |
(2)假设恰好落到竖直位移3R处,则该点的速度方向竖直向下,这不符合平抛运动的规律.设小球离开d出时的速度为vd时,在运动过程中与轨道恰好相碰,即小球的运动轨迹与圆相切.以d点为坐标原点建立如图10坐标系,由平抛运动规律得
x=vdt①
y=
| 1 |
| 2 |
由①②两式得y=
| g | ||
2
|
由解析几何知识得x2+(y-3R)2=R2④
联立③④两式得y2+(
2
| ||
| g |
要使的抛物线与圆相切,则方程⑤的△判别式为零,即△=(
2
| ||
| g |
解得:vd=
(3-2
|
故小球离开轨道d处后,不再碰到轨道,小球离开d出时的速度至少为
(3-2
|
(3)小球从a到c,由动能定理得:
-μmgL-2mgR=
| 1 |
| 2 |
| v | 2 c |
| 1 |
| 2 |
| v | 2 a |
解得vc=2m/s
由牛顿第二定律得
小球在c点前,F1+mg=m
| ||
| R |
解得F1=1N,(方向竖直向下)
小球在c点后,F2-mg=m
| ||
| R |
解得F2=3N,(方向竖直向上)
答:(1)若小球经d处时,对轨道上臂有压力,则它经过b处时的速度满足vb>3
| gR |
(2)为使小球离开轨道d处后,不会再碰到轨道,则小球离开d出时的速度至少为
(3-2
|
(3)则小球对轨道的压力各为F1=1N,(方向竖直向下);F2=3N,(方向竖直向上).
点评:考查动能定理、机械能守恒定律、牛顿第二定律与运动学公式等规律的应用,知道向心力的表达式,同时注意受力分析的研究对象确定.

练习册系列答案
相关题目
 某同学玩“弹珠游戏”装置如图所示,S形管道BC由两个半径为R的
某同学玩“弹珠游戏”装置如图所示,S形管道BC由两个半径为R的