题目内容
如图，长木板ab的b端固定一挡板，木板连同挡板的质量为M="4.0" kg，a、b间距离s="2.0" m.木板位于光滑水平面上.在木板a端有一小物块，其质量m="1.0" kg，小物块与木板间的动摩擦因数μ=0.10，它们都处于静止状态.现令小物块以初速v0="4.0" m/s 沿木板向前滑动，直到和挡板相碰.碰撞后，小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.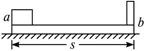
2.4 J
设木板和物块最后共同的速度为v，由动量守恒定律mv0=(m+M)v
全过程损失的机械能为E=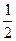
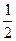mv02-(m+M)v2
全过程由于摩擦生热而损失的机械能E1=μmg·2s
由能量守恒定律得碰撞过程中损失的机械能E2=E-E1
代入数据得E2="2.4" J
全过程损失的机械能为E=
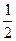mv02-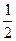(m+M)v2全过程由于摩擦生热而损失的机械能E1=μmg·2s
由能量守恒定律得碰撞过程中损失的机械能E2=E-E1
代入数据得E2="2.4" J
练习册系列答案
阅读快车系列答案
相关题目
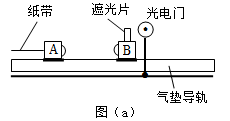
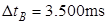，碰撞前后打出的纸带如图（b）所示。
最大为5℅，本实验是否在误差范围内验证了动量守恒定律？写出运算过程。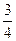
，子弹的质量是物体B的质量的
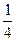，求弹簧压缩到最短时B的速度.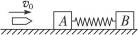
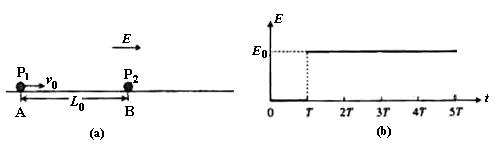
反弹速度大小是碰前速度的一半，P1的质量为m，带电量为q，P2的质量3m，A、B间距为L0．已知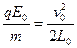
，
．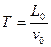