题目内容
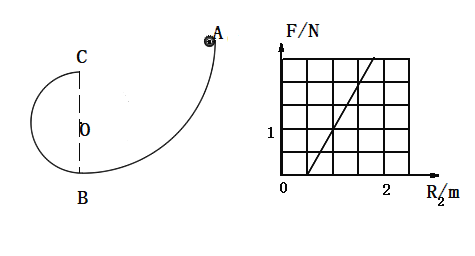
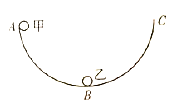
【题目】如图所示，固定在竖直平面内的光滑半圆弧轨道
，其最低点静止有质量为
的小球乙（可视为质点），另一质量为
的小球甲（可视为质点）从圆弧轨道的最高点由静止释放，在轨道的最低点与小球乙发生弹性碰撞。已知半圆弧轨道的半径为
，直径
水平，则下列说法正确的是（ ）
A.要使碰撞后小球乙不离开轨道，小球甲的质量不得大于球乙的质量
B.无论小球甲的质量多大，小球乙都不能离开轨道
C.若两小球的质量相等，则小球乙恰好不能离开圆弧轨道
D.若小球甲的质量足够大，碰撞后小球乙上升的高度可以超过
【答案】AC
【解析】
AB．半圆弧轨道的半径为
，小球甲与乙碰撞前的速度为
，碰后甲与之的速度分别为
，
。两小球发生弹性碰撞，由动量守恒有
，
由机械能守恒定律有
，
解得
，
要使小球乙不能脱离轨道，由机械能守恒定律可知，必有
，
所以
，
故选项A正确，B错误；
C．当两小球的质量相等时，有
，小球乙恰好能到达圆弧轨道右端最高点，选项C正确；
D．当小球甲的质量趋于无穷大时，小球乙的速度趋于
，设碰后小球乙能上升的高度为
，根据机械能守恒有
，
，
解得
，
故选项D错误；
故选AC。
练习册系列答案
相关题目
