题目内容
13. 如图所示,轨道ABC的AB是半径为0.2m的光滑$\frac{1}{4}$圆弧,BC段为高为h=5m的竖直轨道,CD段为水平轨道.一个质量为2kg的小球从A点由静止开始下滑,离开B点做平抛运动,若空气阻力不计,取g=10m/s2.求:
如图所示,轨道ABC的AB是半径为0.2m的光滑$\frac{1}{4}$圆弧,BC段为高为h=5m的竖直轨道,CD段为水平轨道.一个质量为2kg的小球从A点由静止开始下滑,离开B点做平抛运动,若空气阻力不计,取g=10m/s2.求:(1)滑块到达B点时的动能Ek为多少?
(2)小球离开B点后,在CD轨道上的落地点到C的水平距离?
分析 (1)从A到B根据动能定理求得到达B点的动能
(2)从B点开始做平抛运动,根据平抛运动的特点求得水平位移
解答 解:(1)从A到B根据动能定理可知:mgR=Ek-0
代入数据解得:Ek=4J
(2)根据动能可知:Ek=mvB2
代入数据解得:vB=2m/s
从B点做平抛运动,则有:h=$\frac{1}{2}$gt2
解得:t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×5}{10}}s=1s$
水平方向通过的位移为:x=vBt=2m
答:(1)滑块到达B点时的动能Ek为4J
(2)小球离开B点后,在CD轨道上的落地点到C的水平距离为2m
点评 本题主要考查了动能定理和平抛运动,知道平抛运动在 水平方向和竖直方向上的运动规律即可求解

练习册系列答案
相关题目
11.组合体在393km高度绕地球运动过程中,保持不变的物理量有( )
| A. | 周期 | B. | 线速度 | C. | 万有引力 | D. | 向心加速度 |
12.在物理学理论大厦建立的过程中,有许多科学家做出了贡献,关于科学家及其贡献,下列说法正确的是( )
| A. | 伽利略将斜面实验的结果合理外推,发现了行星运动的规律 | |
| B. | 开普勒认为,在高山上以足够大的速度水平抛出一物体,该物体将不会落回地球上 | |
| C. | 奥斯特在实验中观察到电流的磁效应,该效应说明电和磁之间存在联系 | |
| D. | 法拉第根据通电螺线管的磁场和条形磁铁的磁场的相似性,提出了分子电流假说 |
8.如图所示A、B是两列波在同一种介质中传播时在某时刻某范围的波形图,通过对两列波的图象提供的信息分析后可以得出以下结论( )
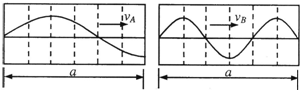

| A. | A、B两列波的波长之比是3:2 | |
| B. | A、B两列波的波速之比是2:1 | |
| C. | A、B两列波的频率之比是1:2 | |
| D. | A波源起振时先向下运动,B波源起振时先向上运动 |
18. 如图所示,同一竖直面内的正方形导线框a、b的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面的匀强磁场区域.开始时,线框b的上边与匀强磁场的下边界重合,线框a的下边到匀强磁场的上边界的距离为l.现将系统由静止释放,当线框b全部进入磁场时,a、b两个线框开始做匀速运动.不计摩擦和空气阻力,则( )
如图所示,同一竖直面内的正方形导线框a、b的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面的匀强磁场区域.开始时,线框b的上边与匀强磁场的下边界重合,线框a的下边到匀强磁场的上边界的距离为l.现将系统由静止释放,当线框b全部进入磁场时,a、b两个线框开始做匀速运动.不计摩擦和空气阻力,则( )
 如图所示,同一竖直面内的正方形导线框a、b的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面的匀强磁场区域.开始时,线框b的上边与匀强磁场的下边界重合,线框a的下边到匀强磁场的上边界的距离为l.现将系统由静止释放,当线框b全部进入磁场时,a、b两个线框开始做匀速运动.不计摩擦和空气阻力,则( )
如图所示,同一竖直面内的正方形导线框a、b的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面的匀强磁场区域.开始时,线框b的上边与匀强磁场的下边界重合,线框a的下边到匀强磁场的上边界的距离为l.现将系统由静止释放,当线框b全部进入磁场时,a、b两个线框开始做匀速运动.不计摩擦和空气阻力,则( )| A. | a、b两个线框匀速运动的速度大小为$\frac{2mgR}{{{B^2}{l^2}}}$ | |
| B. | 线框a从下边进入磁场到上边离开磁场所用时间为$\frac{{3{B^2}{l^3}}}{mgR}$ | |
| C. | 从开始运动到线框a全部进入磁场的过程中,线框a所产生的焦耳热为mgl | |
| D. | 从开始运动到线框a全部进入磁场的过程中,两线框共克服安培力做功为2mgl |
5. 如图,在空间内存在垂直纸面向里的匀强磁场,磁感应强度为B,ab为一水平放置的荧光屏,S为一粒子源,可沿纸面内各个方向发射速度大小相等的带正电粒子,这些粒子质量都为m,电量都为q,这些粒子在纸面内只受磁场力.但不能穿过荧光屏,已知∠Sab=90°,Sa的距离为L,ab长度为2L,则下列判断正确的有( )
如图,在空间内存在垂直纸面向里的匀强磁场,磁感应强度为B,ab为一水平放置的荧光屏,S为一粒子源,可沿纸面内各个方向发射速度大小相等的带正电粒子,这些粒子质量都为m,电量都为q,这些粒子在纸面内只受磁场力.但不能穿过荧光屏,已知∠Sab=90°,Sa的距离为L,ab长度为2L,则下列判断正确的有( )
 如图,在空间内存在垂直纸面向里的匀强磁场,磁感应强度为B,ab为一水平放置的荧光屏,S为一粒子源,可沿纸面内各个方向发射速度大小相等的带正电粒子,这些粒子质量都为m,电量都为q,这些粒子在纸面内只受磁场力.但不能穿过荧光屏,已知∠Sab=90°,Sa的距离为L,ab长度为2L,则下列判断正确的有( )
如图,在空间内存在垂直纸面向里的匀强磁场,磁感应强度为B,ab为一水平放置的荧光屏,S为一粒子源,可沿纸面内各个方向发射速度大小相等的带正电粒子,这些粒子质量都为m,电量都为q,这些粒子在纸面内只受磁场力.但不能穿过荧光屏,已知∠Sab=90°,Sa的距离为L,ab长度为2L,则下列判断正确的有( )| A. | 想要ab下侧的所有位置都能被粒子打到,应使粒子发射速度v≥$\frac{\sqrt{5}BqL}{2m}$ | |
| B. | 想要ab下侧的所有位置都能被粒子打到,应使粒子发射速度v≥$\frac{5BqL}{2m}$ | |
| C. | 想要ab上侧的所有位置都能被粒子打到,应使粒子发射速度v>$\frac{5BqL}{2m}$ | |
| D. | 想要ab上侧的所有位置都能被粒子打到,应使粒子发射速度v>$\frac{\sqrt{5}BqL}{2m}$ |
2.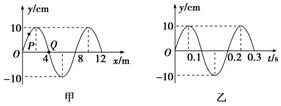 图甲为一列简谐横波在t=0时的波形图,P是平衡位置在x=1.0m处的质点,Q是平衡位置在x=4.0m处的质点;图乙为质点Q的振动图象,下列说法正确的是( )
图甲为一列简谐横波在t=0时的波形图,P是平衡位置在x=1.0m处的质点,Q是平衡位置在x=4.0m处的质点;图乙为质点Q的振动图象,下列说法正确的是( )
 图甲为一列简谐横波在t=0时的波形图,P是平衡位置在x=1.0m处的质点,Q是平衡位置在x=4.0m处的质点;图乙为质点Q的振动图象,下列说法正确的是( )
图甲为一列简谐横波在t=0时的波形图,P是平衡位置在x=1.0m处的质点,Q是平衡位置在x=4.0m处的质点;图乙为质点Q的振动图象,下列说法正确的是( )| A. | 这列波的波长是8.0m,周期是0.2s,振幅是10cm | |
| B. | 在t=0时,质点Q向y轴正方向运动 | |
| C. | 从t=0到t=0.15s,该波沿x轴负方向传播了6m | |
| D. | 从t=0到t=0.15s,质点P通过的路程为30cm | |
| E. | 质点Q简谐运动的表达式为y=0.10sin10πt(国际单位) |
3.将带负电、电荷量为q的检验电荷置于电场中某点,所受电场力大小为F,方向水平向左.移走检验电荷后,该点电场强度( )
| A. | 大小为零,方向水平向左 | B. | 大小为零,方向水平向右 | ||
| C. | 大小为$\frac{F}{q}$,方向水平向左 | D. | 大小为$\frac{F}{q}$,方向水平向右 |
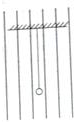 如图所示,该区域存在竖直方向的匀强电场,但方向未知,质量m=2.0×10-3kg的带负电小球用绝缘轻细线竖直地悬于该电场中,当小球带电荷量q=1.0×10-4C时,悬线中的张力T=5×10-3N,则:
如图所示,该区域存在竖直方向的匀强电场,但方向未知,质量m=2.0×10-3kg的带负电小球用绝缘轻细线竖直地悬于该电场中,当小球带电荷量q=1.0×10-4C时,悬线中的张力T=5×10-3N,则: