Question

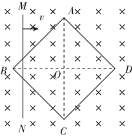
【题目】如图所示，一对磁偏转线圈形成的匀强磁场分布在R = 0.10m的圆形区域内,磁感应强度为0.1T．圆的左端跟y轴相切于直角坐标系的原点O，右端跟足够大的荧光屏MN相切于x轴上A点，置于原点的粒子源沿x轴正方向射出带正电的粒子流，以v =×106m/s射入磁场，粒子的比荷为1×108c/kg，重力不计．求

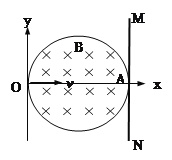
（1）粒子在磁场中运动的时间．

（2）粒子打在荧光屏上的位置距A的距离．

（3）要使粒子打不到荧光屏上，求粒子的速度大小应满足的条件．

Answer 1

【答案】（1）/3×10-7s；（2）×10-1m；（3）速度小于1×106m/s粒子打不到荧光屏上

【解析】

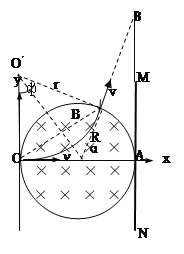
（1）qvB=mv2/r

粒子运动的轨道半径

r=mv/qB=×10-1m

tanΦ/2=R/r=/3

轨迹所对应的圆心角Φ=600

T=2m/qB=2×10-7s

粒子在磁场中运动时间t=T/6=/3×10-7s

如图所示Φ=600

（2）粒子打在荧光屏上的位置距A的距离

L=R×tan600=×10-1m

（3）粒子在磁场中轨道半径为r=R时

粒子沿y轴正方向飞出刚好达不到屏上

qvB=mv2/r

v=qBr/m=1×106m/s

即粒子的速度小于1×106m/s粒子打不到荧光屏上．