题目内容
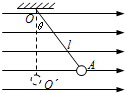（2008?和平区模拟）如图所示，长为l的绝缘细线一端悬于0点，另一端系一质量为m、带电荷+q的小球，小球静止时处于O′点．现将此装置放在水平向右的匀强电场中，小球静止在A点时细线与竖直方向成θ角．求：（1）该匀强电场的电场强度大小．
（2）若将小球从O′点由静止释放，则小球运动到A点时的速度多大？
分析：（1）由题细线向右偏离竖直方向，小球受到的电场力水平向右，根据电场力方向与电场强度方向的关系和根据平衡条件求出电量．
（2）若将小球从O′点由静止释放，则小球运动到A点的过程中，电场力做正功，重力做负功，总功等于小球动能的变化．
（2）若将小球从O′点由静止释放，则小球运动到A点的过程中，电场力做正功，重力做负功，总功等于小球动能的变化．
解答：解：（1）小球在A点受到竖直向下的重力、拉力和水平向右的电场力，根据受力
=tanθ
E=
（2）小球运动到A点的过程中，电场力做正功，重力做负功，根据动能定理E?q
-mgl(1-cosθ)=
mv2
∴v=
答：（1）该匀强电场的电场强度大小E=
．
（2）小球运动到A点时的速度v=
．
| Eq |
| mg |
E=
| mgtanθ |
| q |
（2）小球运动到A点的过程中，电场力做正功，重力做负功，根据动能定理E?q
| l |
| sinθ |
| 1 |
| 2 |
∴v=
|
答：（1）该匀强电场的电场强度大小E=
| mgtanθ |
| q |
（2）小球运动到A点时的速度v=
|
点评：本题是平衡条件与动能定理的综合应用．此题中小球的运动可运用单摆运动类比．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
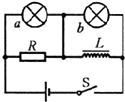（2008?和平区模拟）如图所示，a、b是两个相同的小灯泡，L是一个自感系数很大的线圈，其直流电阻值与电阻R相同，且R小于小灯泡的电阻．闭合开关S，待电路达到稳定后，a、b两灯泡均可发光．由于自感作用，接通和断开开关S，灯泡a和b的发光情况分别是（ ）
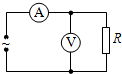（2008?和平区模拟）交流电源电压u=20sin100πt（v），电路中电阻R=10Ω，若不计电表对电路的影响，则途中红电流表、电压表读数分别为（ ）
（2008?和平区模拟）带负电的小物体A放在倾角为θ（sinθ=0.6，cosθ=0.8）的绝缘斜面上．整个斜面处于范围足够大、方向水平向右的匀强电场中，如图所示，物体A的质量为m，电量为-q，与斜面问的动摩擦因数为μ，它在电场中受到的电场力的大小等于重力的一半．物体A在斜面上由静止开始下滑，经时间t后突然在斜面区域加上范围足够大的匀强磁场，磁场方向垂直于纸面．磁感应强度大小为B，此后物体A沿斜面继续下滑距离L后离开斜面．
（2008?和平区模拟）如图所示，在真空区域内，有宽度为L的匀强磁场，磁感应强度为B，磁场方向垂赢纸面向里，MN、PQ是磁场的边界．质量为m，带电量为-q的粒子，先后两次沿着与MN夹角为θ（0＜θ＜90°）的方向垂直磁感线射入匀强磁场B中，第一次，：粒子是经电压U1加速后射入磁场，粒子刚好没能从PQ边界射出磁场．第二次粒子是经电压U2加速后射入磁场，粒子则刚好垂直PQ射出磁场．不计重力的影响，粒子加速前速度认为是零，求：