题目内容
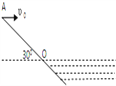
【题目】如图所示,一根弹性细绳颈度系数k=5N/m,将其一端固定,另一端穿过一光滑小孔O且系住一质量为m=1kg的小滑块,滑块放在水平地面上.当细绳竖直时,小孔O到悬点的距离恰为弹性细绳原长,小孔O到正下方水平地面上P点的距离为h=0.5m,滑块与水平地面间的动摩擦因数为μ=0.5,设最大静摩擦力等于滑动摩擦力,弹性细绳始终在其弹性限度内,g=10m/s2 , 求当滑块置于水平面恰好能保持静止时,滑块到P点的最远距离.
【答案】解:当滑块到O点的最远距离时,静摩擦力恰好达到最大值.对滑块受力如图所示,分析可知,

Fcosθ=μFN …①
Fsinθ+FN=mg …②
由胡克定律:F=kx …③
根据几何关系有:xsinθ=h …④
xcosθ=L …⑤
由以上可得:L= ![]() =
= ![]() ;
;
答:滑块到P点的最远距离问哦0.75m.
【解析】本题的难点是根据平衡条件和胡克定律进行求解。

练习册系列答案
相关题目