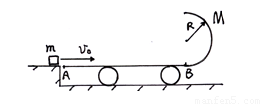
题目内容
有一段长为L,与水平面夹角为θ的斜坡路面,一质量为m的木箱放在斜坡底端,质量为4m的人想沿斜坡将木箱推上坡顶,假设人与路面之间的动摩擦因数为μ(计算中可认为最大静摩擦力等于滑动摩擦力,重力加速度取g),人是沿与斜坡平行的方向用力推木箱的,求:
(1)假设木箱与路面间无摩擦,人推着木箱一起以加速度a向上运动,人受到路面的摩擦力多大?
(2)若木箱与路面间的动摩擦因数也为μ,则人推木箱一起能获得的最大加速度大小是多少?
(3)若木箱与路面间的动摩擦因数也为μ,要将木箱由坡底运送到坡顶,人推木箱一起运动的最短时间是多少?
(1)假设木箱与路面间无摩擦,人推着木箱一起以加速度a向上运动,人受到路面的摩擦力多大?
(2)若木箱与路面间的动摩擦因数也为μ,则人推木箱一起能获得的最大加速度大小是多少?
(3)若木箱与路面间的动摩擦因数也为μ,要将木箱由坡底运送到坡顶,人推木箱一起运动的最短时间是多少?
分析:(1)把人和木箱作为整体,根据牛顿第二定律即可求解;
(2)要使木箱能获得的最大加速度,则人与地面间的摩擦力达到最大值.把人和木箱作为整体,根据牛顿第二定律即可求解;
(3)要使木箱由坡底运送到坡顶,人推木箱的时间最短,则人推木箱必须使木箱以最大加速度向上运行,作用一段时间后,人撤去外力,木箱向上做减速运动,到达坡顶速度恰好为零,根据牛顿第二定律及运动学基本公式列式即可求解.
(2)要使木箱能获得的最大加速度,则人与地面间的摩擦力达到最大值.把人和木箱作为整体,根据牛顿第二定律即可求解;
(3)要使木箱由坡底运送到坡顶,人推木箱的时间最短,则人推木箱必须使木箱以最大加速度向上运行,作用一段时间后,人撤去外力,木箱向上做减速运动,到达坡顶速度恰好为零,根据牛顿第二定律及运动学基本公式列式即可求解.
解答:解:(1)把人和木箱作为整体,根据牛顿第二定律
f-(m+4m)gsinθ=(m+4m)a
得:f=5m(gsinθ+a)
(2)要使木箱能获得的最大加速度,则人与地面间的摩擦力达到最大值.
把人和木箱作为整体,根据牛顿第二定律
μ4mgcosθ-μmgcosθ-(m+4m)gsinθ=(m+4m)am
得:am=
μgcosθ-gsinθ
(3)要使木箱由坡底运送到坡顶,人推木箱的时间最短,则人推木箱必须使木箱以最大加速度向上运行,作用一段时间后,人撤去外力,木箱向上做减速运动,到达坡顶速度恰好为零.
设人撤去外力时,木箱的速度为v,
木箱向上做减速运动的加速度:a2=gsinθ+μgcosθ
对木箱运动全过程有:L=
+
人推木箱最短时间为:tmin=
联立解得:tmin=
答:(1)假设木箱与路面间无摩擦,人推着木箱一起以加速度a向上运动,人受到路面的摩擦力为5m(gsinθ+a);
(2)若木箱与路面间的动摩擦因数也为μ,则人推木箱一起能获得的最大加速度大小是
μgcosθ-gsinθ;
(3)若木箱与路面间的动摩擦因数也为μ,要将木箱由坡底运送到坡顶,人推木箱一起运动的最短时间是
.
f-(m+4m)gsinθ=(m+4m)a
得:f=5m(gsinθ+a)
(2)要使木箱能获得的最大加速度,则人与地面间的摩擦力达到最大值.
把人和木箱作为整体,根据牛顿第二定律
μ4mgcosθ-μmgcosθ-(m+4m)gsinθ=(m+4m)am
得:am=
| 3 |
| 5 |
(3)要使木箱由坡底运送到坡顶,人推木箱的时间最短,则人推木箱必须使木箱以最大加速度向上运行,作用一段时间后,人撤去外力,木箱向上做减速运动,到达坡顶速度恰好为零.
设人撤去外力时,木箱的速度为v,
木箱向上做减速运动的加速度:a2=gsinθ+μgcosθ
对木箱运动全过程有:L=
| v2 |
| 2am |
| v2 |
| 2a2 |
人推木箱最短时间为:tmin=
| v |
| am |
联立解得:tmin=
| 5 |
| 2 |
|
答:(1)假设木箱与路面间无摩擦,人推着木箱一起以加速度a向上运动,人受到路面的摩擦力为5m(gsinθ+a);
(2)若木箱与路面间的动摩擦因数也为μ,则人推木箱一起能获得的最大加速度大小是
| 3 |
| 5 |
(3)若木箱与路面间的动摩擦因数也为μ,要将木箱由坡底运送到坡顶,人推木箱一起运动的最短时间是
| 5 |
| 2 |
|
点评:本题主要考查了牛顿第二定律及运动学基本公式的直接应用,要求同学们能正确对物体进行受力分析,难度适中.

练习册系列答案
相关题目
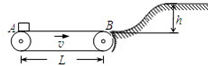 为了节能,某货场设计了如图所示的送货装置,长为L的水平传送带右端B与一光滑弧面相连,弧面顶端为储货平台,将货物无初速度轻放在传送带左端A,通过传送带到达B端时具有一定动能,货物可以利用此动能滑上储货平台,平台离传送带高h,在安装调试时传送带以某一速度匀速运动,工人发现货物只能上滑到
为了节能,某货场设计了如图所示的送货装置,长为L的水平传送带右端B与一光滑弧面相连,弧面顶端为储货平台,将货物无初速度轻放在传送带左端A,通过传送带到达B端时具有一定动能,货物可以利用此动能滑上储货平台,平台离传送带高h,在安装调试时传送带以某一速度匀速运动,工人发现货物只能上滑到 如图所示,在光滑的水平面上有一段长为L、质量分布均匀的绳子,绳子在水平向左的恒力F作用下做匀加速直线运动.绳子上某一点到绳子右端的距离为x,设该处的张力为T,则能正确描述T与x之间的关系的图象是( )
如图所示,在光滑的水平面上有一段长为L、质量分布均匀的绳子,绳子在水平向左的恒力F作用下做匀加速直线运动.绳子上某一点到绳子右端的距离为x,设该处的张力为T,则能正确描述T与x之间的关系的图象是( )