Question

【题目】英国物理学家胡克发现，金属丝或金属杆在弹性限度内的伸长与拉力成正比，这就是著名的胡克定律．这个发现为后人对材料的研究奠定了重要的基础．现有一根用新材料制成的金属杆，长为4m，横截面积为0.8cm2，设计要求它受到拉力后的伸长不超过原长的1/1000，由于这一拉力很大，杆又较长，直接测量有困难，就选用同种材料制成样品进行测试，通过测试取得的数据如下：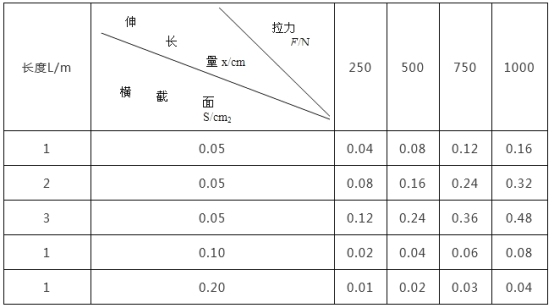

(1)根据测试结果，推导出线材伸长量x与材料的长度L、材料的横截面积S与拉力F的函数关系为____．

(2)在寻找上述关系中，你运用哪种科学研究方法？________.

(3)通过对样品的测试，求出新材料制成的金属细杆能承受的最大拉力约________．

Answer 1

【答案】x＝k控制条件法104N

【解析】

（1）由表格知：
a、当受到的拉力F、横截面积S一定时，伸长量x与样品长度L成正比；①
b、当受到的拉力F、样品长度L一定时，伸长量x与横截面积S成反比；②
c、当样品长度L、横截面积S一定时，伸长量x与受到的拉力F成正比；③
由①②③三个结论，可以归纳出，x与L、S、F之间存在一定量的比例关系，设这个比值为k，那么有：线材伸长量x与材料的长度L、材料的横截面积S与拉力F的函数关系为（k为常数）
（2）由题可知伸长量x与样品的长度、横截面积、所受拉力都有关系，涉及的变量较多，因此采用“控制变量法”来确定它们之间的正、反比关系．
（3）根据图表提供数据代入
解得：k=×10-10m2/N．
由题意知：待测金属杆M承受最大拉力时，其伸长量为原来的1/1000，即4×10-3m；
此时 S=0.8cm2=8×10-5m2，L=4m；代入上面的公式
解得：F=10000N．