题目内容
如图所示，用丝线吊一个质量为m的带电（绝缘）小球处于匀强磁场中，空气阻力不计，当小球分别从A点和B点向最低点O运动且两次经过O点时（ ）分析：带电小球在重力与拉力及洛伦兹力共同作用下，绕固定点做圆周运动，由于拉力与洛伦兹力始终垂直于速度方向，它们对小球不做功．因此仅有重力作功，则有机械能守恒．从而可以确定动能是否相同，并由此可确定拉力与洛伦兹力．最后由向心加速度公式来确定是否相同．
解答：解：A、由题意可知，拉力与洛伦兹力对小球不做功，仅仅重力作功，则小球机械能守恒，所以小球分别从A点和B点向最低点O运动且两次经过O点时的动能相同，故A正确；
B、由A选项可知，速度大小相等，则根据牛顿第二定律可知，由于速度方向不同，导致产生的洛伦兹力的方向也不同，则拉力的大小也不同，故B错误；
C、由于小球的运动方向不同，则根据左手定则可知，洛伦兹力的方向不同，但大小却相同．故C错误；
D、根据a=
，可知小球的向心加速度大小相同，且方向指向固定点，即加速度相同，故D正确；
故选：AD
B、由A选项可知，速度大小相等，则根据牛顿第二定律可知，由于速度方向不同，导致产生的洛伦兹力的方向也不同，则拉力的大小也不同，故B错误；
C、由于小球的运动方向不同，则根据左手定则可知，洛伦兹力的方向不同，但大小却相同．故C错误；
D、根据a=
| v2 |
| r |
故选：AD
点评：本题考查对小球进行受力分析，并得出力做功与否，根据机械能守恒定律来解题是突破口，同时注意洛伦兹力方向随着速度的方向不同而不同．最后由牛顿第二定律来考查向心力与向心加速度．
练习册系列答案
相关题目
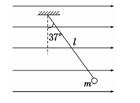
用一根长为l的丝线吊着一质量为m带电荷量为q的小球，小球静止在水平向右的匀强电场中，如图所示，丝线与竖直方向成370角．现突然将该电场方向变为向下但大小不变，不考虑因电场的改变而带来的其他影响（重力加速度为g），求：
用一根长为L的丝线吊着一质量为m、带电荷量为q的小球，小球静止在水平向右的匀强电场中，如图所示，丝线与竖直方向成37°角．现突然将该电场方向变为向竖直上，但大小不变，不考虑因电场的改变而带来的其他影响（重力加速度为g，sin37°=0.6，cos37°=0.8），如图所示，求：
