题目内容
如图所示.在一矩形区域内,不加磁场时,不计重力的带电粒子以某一初速度垂直左边界射入,穿过此区域的时间为t,若加上磁感应强度为B水平向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出时偏离原方向60°,利用以上数据可求出下列物理量中的哪几个( )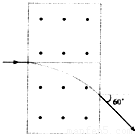
A.带电粒子的比荷
B.带电粒子在磁场中运动的周期
C.带电粒子的初速度
D.带电粒子在磁场中运动的半径
【答案】分析:这种由已知量,来确定可以求那些量的题目,要从给定情形中的已知量涉及的公式,来进行尝试变化,组合.最终能消掉公式中未知量的,就是可以求出的量.而在尝试变化,组合之后仍不能消掉的,即为求不出来的.
解答:解:
由带电粒子在磁场中运动的偏转角可知,带电粒子运动轨迹所对的圆心角为60°,由几何关系得磁场宽度d=rsin60°=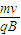 sin60°,又由未加磁场时有d=vt,所以可求得比荷
sin60°,又由未加磁场时有d=vt,所以可求得比荷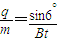 ,故A正确
,故A正确
周期: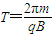 可求出,故B正确
可求出,故B正确
因初速度未知,无法求出CD,故C、D错误.
故选AB
点评:这种题目需要公式很熟练,且组合变化条理,才能得到哪些是可求的,哪些是不可求的.综合应用公式得能力要求比较高.
解答:解:
由带电粒子在磁场中运动的偏转角可知,带电粒子运动轨迹所对的圆心角为60°,由几何关系得磁场宽度d=rsin60°=
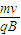 sin60°,又由未加磁场时有d=vt,所以可求得比荷
sin60°,又由未加磁场时有d=vt,所以可求得比荷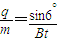 ,故A正确
,故A正确周期:
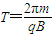 可求出,故B正确
可求出,故B正确因初速度未知,无法求出CD,故C、D错误.
故选AB
点评:这种题目需要公式很熟练,且组合变化条理,才能得到哪些是可求的,哪些是不可求的.综合应用公式得能力要求比较高.

练习册系列答案
相关题目
 如图所示,在纸平面内建立的直角坐标系xoy,在第一象限的区域存在沿y轴正方向的匀强电场.现有一质量为m,电量为e的电子从第一象限的某点P(L,
如图所示,在纸平面内建立的直角坐标系xoy,在第一象限的区域存在沿y轴正方向的匀强电场.现有一质量为m,电量为e的电子从第一象限的某点P(L,
 ,ad与ac夹角为
,ad与ac夹角为 =300。一质量为
=300。一质量为 带电量为
带电量为 的粒子以速度V0从Ⅰ区边缘a点沿ad方向射入磁场,随后粒子经过ac与bd交点o进入Ⅱ区(粒子重力不计)。
的粒子以速度V0从Ⅰ区边缘a点沿ad方向射入磁场,随后粒子经过ac与bd交点o进入Ⅱ区(粒子重力不计)。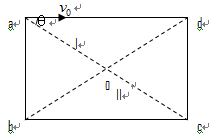
 的方向和大小
的方向和大小 应满足的条件
应满足的条件 ,ad与ac夹角为
,ad与ac夹角为 =300。一质量为
=300。一质量为 带电量为
带电量为 的粒子以速度V0从Ⅰ区边缘a点沿ad方向射入磁场,随后粒子经过ac与bd交点o进入Ⅱ区(粒子重力不计)。
的粒子以速度V0从Ⅰ区边缘a点沿ad方向射入磁场,随后粒子经过ac与bd交点o进入Ⅱ区(粒子重力不计)。
 的方向和大小
的方向和大小 应满足的条件
应满足的条件