题目内容
5. 如图,一不可伸长的轻绳上端悬挂于O点,下端系一质量m=1.0kg的小球.现将小球拉到A点(保持绳绷直)由静止释放,当它经过B点时绳恰好被拉断,小球平拋后落在水平地面上的C点.地面上的D点与OB在同一竖直线上,已知绳长L=1.0m,B点离地高度H=3.2m,A、B两点的高度差h=0.8m,重力加速度g取10m/s2,不计空气影响,求:
如图,一不可伸长的轻绳上端悬挂于O点,下端系一质量m=1.0kg的小球.现将小球拉到A点(保持绳绷直)由静止释放,当它经过B点时绳恰好被拉断,小球平拋后落在水平地面上的C点.地面上的D点与OB在同一竖直线上,已知绳长L=1.0m,B点离地高度H=3.2m,A、B两点的高度差h=0.8m,重力加速度g取10m/s2,不计空气影响,求:(1)地面上DC两点间的距离s;
(2)轻绳所受的最大拉力大小.
分析 (1)从A到B由动能定理可得B位置时的速度,之后做平抛运动,由平抛规律求解;
(2)在B位置,绳的拉力和重力的合力提供向心力,由牛顿第二定律可求轻绳所受的最大拉力大小.
解答 解:(1)小球从A到B过程机械能守恒,有 mgh=$\frac{1}{2}$mvB2①
小球从B到C做平抛运动,在竖直方向上有 H=$\frac{1}{2}$gt2②
在水平方向上有 s=vBt③
由①②③式解得s=3.2 m④
(2)小球下摆到达B点时,绳的拉力和重力的合力提供向心力,有F-mg=m$\frac{v}{L}$⑤
由①⑤式解得F=26 N 
根据牛顿第三定律:轻绳所受的最大拉力为26 N.
答:(1)地面上DC两点间的距离是3.2m;
(2)轻绳所受的最大拉力大小是26N.
点评 本题为圆周和平抛模型的组合,解答的关键是建立物体运动的情境,寻找物理模型,再结合相应的情景列式.

练习册系列答案
相关题目
15.一观察者站在第一节车厢前端,当列车从静止开始作匀加速运动时( )
| A. | 每节车厢末端经过观察者的速度之比是1:$\sqrt{2}$:$\sqrt{3}$:… | |
| B. | 每节车厢经过观察者所经历时间之比是1:2:3:… | |
| C. | 在相等时间里经过观察者的车厢数之比是1:3:5:… | |
| D. | 在相等时间里经过观察者的车厢数之比是1:2:3:… |
16.甲乙两公共汽车站相向发车,一人在街上匀速前进,发现每隔4分钟迎面开来一辆车,每隔12分钟从背后开来一辆车.如果两站发车时间相同,各车车速相同,则两车站发车的间隔时间为( )
| A. | 2分钟 | B. | 4 分钟 | C. | 6分钟 | D. | 8分钟 |
13.下列物理量是矢量的是( )
| A. | 磁感应强度 | B. | 电动势 | C. | 电势 | D. | 磁通量 |
20.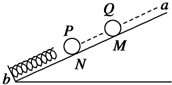 如图所示,绝缘弹簧的下端固定在斜面底端,弹簧与斜面平行,带电小球Q(可视为质点)固定在光滑绝缘斜面上的M点,且在通过弹簧中心的直线ab上.现把与Q大小相同,带电性也相同的小球P,从直线ab上的N点由静止释放,在小球P与弹簧接触到速度变为零的过程中( )
如图所示,绝缘弹簧的下端固定在斜面底端,弹簧与斜面平行,带电小球Q(可视为质点)固定在光滑绝缘斜面上的M点,且在通过弹簧中心的直线ab上.现把与Q大小相同,带电性也相同的小球P,从直线ab上的N点由静止释放,在小球P与弹簧接触到速度变为零的过程中( )
 如图所示,绝缘弹簧的下端固定在斜面底端,弹簧与斜面平行,带电小球Q(可视为质点)固定在光滑绝缘斜面上的M点,且在通过弹簧中心的直线ab上.现把与Q大小相同,带电性也相同的小球P,从直线ab上的N点由静止释放,在小球P与弹簧接触到速度变为零的过程中( )
如图所示,绝缘弹簧的下端固定在斜面底端,弹簧与斜面平行,带电小球Q(可视为质点)固定在光滑绝缘斜面上的M点,且在通过弹簧中心的直线ab上.现把与Q大小相同,带电性也相同的小球P,从直线ab上的N点由静止释放,在小球P与弹簧接触到速度变为零的过程中( )| A. | 小球P的速度先增大后减小 | |
| B. | 系统的机械能守恒 | |
| C. | 小球P的动能、重力势能、电势能与弹簧的弹性势能的总和增大 | |
| D. | 小球P速度最大时所受弹力与库仑力的合力为零 |
10.关于物理学发展过程的认识,下列说法中正确的是( )
| A. | 伽利略根据理想斜面实验,提出了惯性定律 | |
| B. | 开普勒认为所有行星绕太阳运动的轨道都是椭圆 | |
| C. | 亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快 | |
| D. | 牛顿用实验的方法测出万有引力常量 |
14.质点沿x轴正方向运动,在t=2s时刻它的位置坐标为x1=-4m,t=6s时刻它的位置坐标为x2=6m,则在这段时间内质点的位置变化、平均速度V分别是多少( )
| A. | △X=10m | B. | △X=-10m | C. | V=2.5m/s | D. | V=-2.5m/s |
 如图所示,在光滑平直轨道上有A、B、C三个物体,其中A的质量为2m,B、C质量均为m,物体A以速度v0向右运动,物体B、C均静止.A与B发生弹性碰撞,B、C碰撞后粘合在一起.求:
如图所示,在光滑平直轨道上有A、B、C三个物体,其中A的质量为2m,B、C质量均为m,物体A以速度v0向右运动,物体B、C均静止.A与B发生弹性碰撞,B、C碰撞后粘合在一起.求: