题目内容
6.一辆客车从静止开始以加速度a=1.0m/s2做匀加速直线运动的同时,在车的后面离车为s=30m远的地方有一乘客正以某一速度v在匀速追赶这辆客车.(1)要能追上这辆车,乘客的速度至少是多少?
(2)若已知司机通过观后镜能看到车后追赶的乘客离车的最远距离为s0=20m(即该乘客离车距离大于20m时超出司机的视线范围),且需要在视线中保留的时间不少于t0=1.0s,这样司机才能发现该乘客,并制动客车使车停下来.该乘客要想乘坐上这辆客车,其追赶客车的速度的最小值是多少?
分析 (1)当人与车的速度相等时,人恰好追上车,此时人的速度最小,应用匀变速直线运动的速度公式、位移公式,匀速运动的位移公式可以求出人的速度.
(2)设乘客经过t时间与客车车头的位移为s0,通过位移关系求出运动的时间,时间有两个值,在这两个时间之间,乘客与客车车头的位移小于s0,则两个时间之差要保证大于等于t0,根据该关系求出乘客速度的最小值.
解答 解:(1)若人与车速度相同时恰能追上汽车,
车的速度:v=at,
人的位移:s人=vt,
车的位移:s车=$\frac{1}{2}$at2,
人追上车时:s人-s车=s,
代入数据解得:v=2$\sqrt{15}$m/s;
(2)从客车由静止开始计时,经时间t,
客车前进:s1=$\frac{1}{2}$at2 ①
乘客行走的距离为:s2=vt ②
由题意知:s1+s-s2=s0 ③
由①②③联立得:$\frac{1}{2}$at2+s-vt-s0=0,
整理得:t=$\frac{v±\sqrt{{v}^{2}-2a(s-{s}_{0})}}{a}$,
两根之差:△t=t2-t1=$\frac{v+\sqrt{{v}^{2}-2a(s-{s}_{0})}}{a}$-$\frac{v-\sqrt{{v}^{2}-2a(s-{s}_{0})}}{a}$,
根据题意,有:△t≥t0,代入数据解得:v≥4.5m/s;
答:(1)要能追上这辆车,乘客的速度至少是2$\sqrt{15}$m/s;
(2)该乘客要想乘坐上这辆客车,其追赶客车的速度的最小值是4.5m/s.
点评 本题考查了追及问题,分析清楚物体的运动过程,找出两物体间追及的条件是正确解题的前提与关键;该题属于运动学中的较难题,关键抓住乘客经过时间t与客车车头的位移为s0,还要注意乘客与客车车头位移在s0之内的时间差大于等于t0.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案| A. | 衰变和裂变都能自发发生 | |
| B. | 衰变和裂变都不能自发发生 | |
| C. | 衰变能自发发生而裂变不能自发发生 | |
| D. | 衰变不能自发发生而裂变能自发发生 |
 如图所示是一半径为R的玻璃球体,0为球心,AB为水平直径,M点是玻璃球的最高点,来自B点的光线BD从D点射出,出射光线平行于AB,已知∠ABD=30°,光在真空中的传播速度为c,则( )
如图所示是一半径为R的玻璃球体,0为球心,AB为水平直径,M点是玻璃球的最高点,来自B点的光线BD从D点射出,出射光线平行于AB,已知∠ABD=30°,光在真空中的传播速度为c,则( )| A. | 此玻璃的折射率为$\frac{2}{3}$$\sqrt{3}$ | |
| B. | 光线从B传到D的时间为$\frac{3R}{c}$ | |
| C. | 若增大∠ABD,光线不可能在DM段发生全反射现象 | |
| D. | 若减小∠ABD,从AD段射出的光线均平行于AB |
| A. | 库仑在研究电荷之间相互作用时提出了“电场”的概念 | |
| B. | 1831年法拉第首先发现了电磁感应现象 | |
| C. | 电流强度的概念是由I=$\frac{U}{R}$采用比值法定义的 | |
| D. | 用质点来代替实际物体的研究方法是等效替代法 |
| A. | 关于原子核内部信息,最早来自天然放射性现象 | |
| B. | 结合能越大的原子核越稳定 | |
| C. | 目前核电站中主要利用的是轻核聚变产生的核能来发电 | |
| D. | 在核反应堆中常用的“慢化剂”有石墨、重水和普通水 | |
| E. | 在铀核的裂变中,当铀块的体积小于“临界体积”时,不能发生链式反应 |
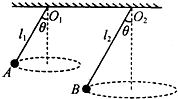 如图所示,两个相同的小球A、B用长度分别为l1、l2的细线悬挂在天花板的O1,O2点,两球在水平面内做匀速圆周运动,两根细线与竖直轴夹角均为θ.设A,B两球的线速度分别为vA、vB,角速度分别为ωA、ωB,加速度分别为aA、aB,两根细线的拉力分别为FA、FB,则( )
如图所示,两个相同的小球A、B用长度分别为l1、l2的细线悬挂在天花板的O1,O2点,两球在水平面内做匀速圆周运动,两根细线与竖直轴夹角均为θ.设A,B两球的线速度分别为vA、vB,角速度分别为ωA、ωB,加速度分别为aA、aB,两根细线的拉力分别为FA、FB,则( )| A. | vA>vB | B. | ωA>ωB | C. | aA=aB | D. | FA<FB |
 如图甲所示为一简谐波在t=0时刻的图象,图乙所示为x=4m处的质点P的振动图象,则下列判断正确的是( )
如图甲所示为一简谐波在t=0时刻的图象,图乙所示为x=4m处的质点P的振动图象,则下列判断正确的是( )| A. | 这列波的波速是4m/s | |
| B. | 这列波的传播方向沿x正方向 | |
| C. | 从t=0时刻开始计时,P点的振动方程为y=0.2sin(πt+$\frac{π}{2}$)m | |
| D. | 从t=0时刻开始计时,P点的振动方程为y=0.2sin(πt+π)m |
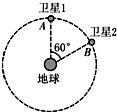 北斗导航系统中两颗工作卫星即卫星1和卫星2在同一轨道上绕地心做匀速圆周运动,轨道半径为r,如图所示,某时刻卫星1和卫星2分别位于轨道上的A、B两位置(卫星与地球连线的夹角为60°).若两卫星均按顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列说法正确的是( )
北斗导航系统中两颗工作卫星即卫星1和卫星2在同一轨道上绕地心做匀速圆周运动,轨道半径为r,如图所示,某时刻卫星1和卫星2分别位于轨道上的A、B两位置(卫星与地球连线的夹角为60°).若两卫星均按顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列说法正确的是( )| A. | 地球对卫星1和卫星2的万有引力大小相等 | |
| B. | 卫星1由位置A运动到位置B的过程中万有引力做正功 | |
| C. | 卫星l由位置A运动到位置B所需的时间为$\frac{πr}{3R}\sqrt{\frac{r}{g}}$ | |
| D. | 若卫星l向后喷气,则一定能追上卫星2 |
