题目内容
16.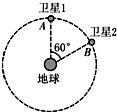 北斗导航系统中两颗工作卫星即卫星1和卫星2在同一轨道上绕地心做匀速圆周运动,轨道半径为r,如图所示,某时刻卫星1和卫星2分别位于轨道上的A、B两位置(卫星与地球连线的夹角为60°).若两卫星均按顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列说法正确的是( )
北斗导航系统中两颗工作卫星即卫星1和卫星2在同一轨道上绕地心做匀速圆周运动,轨道半径为r,如图所示,某时刻卫星1和卫星2分别位于轨道上的A、B两位置(卫星与地球连线的夹角为60°).若两卫星均按顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列说法正确的是( )| A. | 地球对卫星1和卫星2的万有引力大小相等 | |
| B. | 卫星1由位置A运动到位置B的过程中万有引力做正功 | |
| C. | 卫星l由位置A运动到位置B所需的时间为$\frac{πr}{3R}\sqrt{\frac{r}{g}}$ | |
| D. | 若卫星l向后喷气,则一定能追上卫星2 |
分析 无论用万有引力表达式,还是用万有引力提供向心力的各种形式的表达式,都需知道卫星的质量,才能求万有引力.
万有引力提供向心力,始终与速度方向垂直.
由万有引力提供向心力的周期表达式,可得周期,进而可得卫星l由位置A运动到位置B所需的时间.
若卫星1向后喷气,则其速度会增大,卫星1将做离心运动
解答 解:A、无论用万有引力表达式,还是用万有引力提供向心力的各种形式的表达式,都需知道卫星的质量,才能求万有引力,卫星1、2的质量未知,所以地球对二者的万有引力大小不确定,故A错误;
B、卫星做匀速圆周运动,万有引力提供向心力,始终与速度方向垂直,所以万有引力不做功,故B错误;
C、由万有引力提供向心力的周期表达式,可得:$T=2π\sqrt{\frac{{r}^{3}}{GM}}$=$2π\sqrt{\frac{r}{g}}$,由A运动到B用时t=$\frac{60°}{360°}T$=$\frac{πr}{3R}\sqrt{\frac{r}{g}}$,则C正确
D、卫星1 向后喷气加速将要离心运动,故不能追上卫星2,故D错误.
故选:C
点评 关于卫星运动,要熟练应用万有引力提供向心力的各种表达形式;熟知卫星的变轨

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.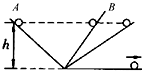 如图所示,伽利略用两个对接的斜面,一个斜面A固定,让小球从固定斜面上由静止滚下,又滚上另一个倾角可以改变的斜面B,如果没有摩擦,小球将上升到原来的高
如图所示,伽利略用两个对接的斜面,一个斜面A固定,让小球从固定斜面上由静止滚下,又滚上另一个倾角可以改变的斜面B,如果没有摩擦,小球将上升到原来的高
度,减小斜面倾角重复实验,直到斜面倾角为零.伽利略设计这个实验的目的是为了说明( )
 如图所示,伽利略用两个对接的斜面,一个斜面A固定,让小球从固定斜面上由静止滚下,又滚上另一个倾角可以改变的斜面B,如果没有摩擦,小球将上升到原来的高
如图所示,伽利略用两个对接的斜面,一个斜面A固定,让小球从固定斜面上由静止滚下,又滚上另一个倾角可以改变的斜面B,如果没有摩擦,小球将上升到原来的高度,减小斜面倾角重复实验,直到斜面倾角为零.伽利略设计这个实验的目的是为了说明( )
| A. | 日常生活中,不存在摩擦时,物体的运动情形 | |
| B. | 如果没有摩擦,小球将运动到与释放时相同的高度 | |
| C. | 如果没有摩擦,物体运动时机械能守恒 | |
| D. | 力不是维持物体运动状态的原因 |
4.光在科学技术、生产和生活中有着广泛的应用,下列说法正确的是( )
| A. | 用透明的标准平面样板检查光学平面的平整程度是利用光的偏振现象 | |
| B. | 用三棱镜观察白光看到的彩色图样是利用光的衍射现象 | |
| C. | 在光导纤维束内传送图象是利用光的全反射现象 | |
| D. | 光学镜头上的增透膜是利用光的干涉现象 | |
| E. | 在光的双缝干涉实验中,若仅将入射光由红光改为绿光,则干涉条纹间距变窄 |
1. 某质点做加速度随时间周期性变化的变加速直线运动,加速度随时间变化关系如图所示,下列关于该质点的运动的叙述中正确的是( )
某质点做加速度随时间周期性变化的变加速直线运动,加速度随时间变化关系如图所示,下列关于该质点的运动的叙述中正确的是( )
 某质点做加速度随时间周期性变化的变加速直线运动,加速度随时间变化关系如图所示,下列关于该质点的运动的叙述中正确的是( )
某质点做加速度随时间周期性变化的变加速直线运动,加速度随时间变化关系如图所示,下列关于该质点的运动的叙述中正确的是( )| A. | 质点可能在直线上作往复运动 | |
| B. | 质点一定做一直向正方向的直线运动 | |
| C. | t=0.1s时,质点的速度最大 | |
| D. | t=0.2s时,质点的位移最大 |
5. a、b两车在同一直线上做匀加速直线运动,v-t图象如图所示,在15s末两车在途中相遇,由图象可知( )
a、b两车在同一直线上做匀加速直线运动,v-t图象如图所示,在15s末两车在途中相遇,由图象可知( )
 a、b两车在同一直线上做匀加速直线运动,v-t图象如图所示,在15s末两车在途中相遇,由图象可知( )
a、b两车在同一直线上做匀加速直线运动,v-t图象如图所示,在15s末两车在途中相遇,由图象可知( )| A. | a车的速度变化比b车快 | B. | 出发前a车在b车之前75m处 | ||
| C. | 出发前b车在a车之前150m处 | D. | 相遇前a、b两车的最远距离为150m |

 据《环球时报》报道:“神舟”三号飞船发射升空后,美国方面立即组织力量进行追踪,但英国权威军事刊物《简史防务周刊》评论说,“这使美国感到某种程度的失望”.美国追踪失败的原因是“神舟”三号在发射数小时后,进行了变轨操作,后期轨道较初始轨道明显偏低,如图所示,开始飞船在轨道1上运行几周后,在Q点开启发动机喷射高速气体使飞船减速,随即关闭发动机,飞船接着沿椭圆轨道2运行,到达P点再次开启发动机,使飞船速度变为符合圆轨道3的要求,进入轨道3后绕地球做圆周运动,则飞船在轨道2上从Q点到P点的过程中,运行速率将( )
据《环球时报》报道:“神舟”三号飞船发射升空后,美国方面立即组织力量进行追踪,但英国权威军事刊物《简史防务周刊》评论说,“这使美国感到某种程度的失望”.美国追踪失败的原因是“神舟”三号在发射数小时后,进行了变轨操作,后期轨道较初始轨道明显偏低,如图所示,开始飞船在轨道1上运行几周后,在Q点开启发动机喷射高速气体使飞船减速,随即关闭发动机,飞船接着沿椭圆轨道2运行,到达P点再次开启发动机,使飞船速度变为符合圆轨道3的要求,进入轨道3后绕地球做圆周运动,则飞船在轨道2上从Q点到P点的过程中,运行速率将( )