题目内容
20.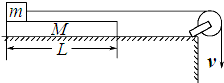 如右图所示,一块质量为M=2kg?长为L=1m的匀质木板放在很长的光滑水平桌面上,板的左端有一质量为m=0.5kg的物块,物块上连接一根很长的细绳,细绳跨过位于桌面边缘的定滑轮,某人以速度v=1m/s向下拉绳,物块最多只能到达板的中点,而且此时板的右端尚未到达桌边定滑轮处.g取10m/s2,求:
如右图所示,一块质量为M=2kg?长为L=1m的匀质木板放在很长的光滑水平桌面上,板的左端有一质量为m=0.5kg的物块,物块上连接一根很长的细绳,细绳跨过位于桌面边缘的定滑轮,某人以速度v=1m/s向下拉绳,物块最多只能到达板的中点,而且此时板的右端尚未到达桌边定滑轮处.g取10m/s2,求:(1)物块与板间的动摩擦因数μ1;
(2)若板与桌面间有摩擦,为使物块能到板的右端,板与桌面的动摩擦因数μ2的范围.
分析 (1)木板先做加速运动们最后做匀速运动,当两者速度达到相等时,木块相对于木板不再发生运动,利用运动学公式及牛顿第二定律即可求得摩擦因数;
(2)当木块刚好达到木板最右端时,由牛顿运动学公式及牛顿第二定律即可求的最小摩擦因数;
解答 解:(1)若人以恒定速度v=1m/s向下匀速拉绳,木板先向右做匀加速运动,物块到达板的中点后,物块和木板一起以1m/s匀速.
设M加速时间为t1,则m向右位移为x1=vt1
木板向右的位移为x2=$\frac{v}{2}t$1
由题意得x1-x2=$\frac{L}{2}$
由以上三式代入数据可得t1=1s
M加速度:$a=\frac{v}{t_1}=1m/{s^2}$
由牛顿第二定律得:μ1mg=Ma
代入数据解得:μ1=0.4
(2)如果板与桌面有摩擦,因为M与桌面摩擦因数越大,m越易从右端滑下,所以当m滑到M右端两者刚好共速时摩擦因数最小,设为μ0,且物块在板上滑行的时间为t2.
对木板由牛顿第二定律得:μ1mg-μ0(M+m)g=Ma1,
而v=a1t2
解得:${t_2}=\frac{Mv}{{{μ_1}mg-{μ_0}(M+m)g}}$
又设物块从板的左端运动到右端的时间为t3则$v{t_2}-\frac{v}{2}{t_2}=L$,
得:${t_2}=\frac{2L}{v}$
解得:${μ_0}=\frac{{M{v^2}}}{2(M+m)gL}=0.04$.
所以为了使物块能到达板的右端,板与桌面间的摩擦因数μ2≥0.04
答:(1)物块与板间的动摩擦因数为0.4.
(2)板与桌面的动摩擦因数μ2的范围为μ2≥0.04.
点评 分析求出物体运动过程、应用牛顿第二定律、运动学公式的公式即可正确解题.难度中等.

练习册系列答案
相关题目
10.下列说法正确的( )
| A. | 放射性元素的半衰期与压力、温度无关 | |
| B. | 德布罗意认为一切物体都具有波粒二象性 | |
| C. | 处于n=3的一个氢原子回到基态时一定会辐射三种频率的光子 | |
| D. | 黑体辐射电磁波的强度按波长分布只与温度有关 |
8.一同学家住在15层高级的顶楼,他想研究一下电梯上升的运动过程,某天他乘电梯上楼时捎带了一个质量未知的重物和一个量程足够大的台秤,他将重物放在台秤上,电梯从第1层开始启动,一直运动到第15层停止,在这个过程中,他记录了台秤在不同时段内的读数如表所示,根据表格中的数据,下列说法正确的是(g=10m/s2)( )
| 时间/s | 台秤示数/N |
| 电梯启动前 | 50.0 |
| 0~3.0 | 58.0 |
| 3.0~13.0 | 50.0 |
| 13.0~19.0 | 46.0 |
| 19.0以后 | 50.0 |
| A. | 该同学根据台秤的示数可算了此重物的质量 | |
| B. | 0-0.3s内,重物处于失重状态 | |
| C. | 13.0-19.0s内,重物处于超重状态 | |
| D. | 该同学根据台秤的示数可算出电梯在最初加速阶段和最后减速阶段的加速度大小 |
15.有一质点从t=0开始由原点出发沿直线运动,其运动的速度-时间图象如图所示,则质点( )
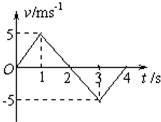

| A. | 前两秒加速度为5 m/s2 | B. | t=2s时,离原点的距离最大 | ||
| C. | t=3s时,离原点的距离最大 | D. | t=4s时,离原点的距离最大 |
5.在“探究小车速度随时间变化的规律”实验中,下列说法正确的是( )
| A. | 先释放纸带,再接通电源 | |
| B. | 先接通电源,后释放纸带 | |
| C. | 纸带上打点越密集说明纸带运动速度越大 | |
| D. | 利用打出的纸带可以求出打下某点时纸带的瞬时速度 |
12.如图所示,实线表示一簇关于x轴对称的等势面,在轴上有A、B两点,则( )


| A. | A点场强小于B点场强 | B. | A点场强方向指向x轴负方向 | ||
| C. | A点场强大于B点场强 | D. | A点电势高于B点电势 |
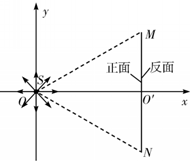 如图所示,在直角坐标系xOy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的正电粒子,位于y轴的右侧垂直于x轴有一长度为L的很薄的荧光屏MN,荧光屏正反两侧均涂有荧光粉,MN与x轴交于O′点.已知三角形MNO为正三角形,放射源S射出的粒子质量为m,带电荷量为q,速度大小为v,不计粒子的重力.
如图所示,在直角坐标系xOy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的正电粒子,位于y轴的右侧垂直于x轴有一长度为L的很薄的荧光屏MN,荧光屏正反两侧均涂有荧光粉,MN与x轴交于O′点.已知三角形MNO为正三角形,放射源S射出的粒子质量为m,带电荷量为q,速度大小为v,不计粒子的重力. 如图,一个水平放置的导体框架,宽度L=2m,接有电阻R=4Ω,设匀强磁场和框架平面垂直,磁感应强度B=1T,方向如图.今有一导体棒ab跨放在框架上,并能无摩擦地沿框滑动,框架及导体ab电阻均不计,当ab受到一平行于导轨的水平外力F而以v=4m/s的速度向右匀速滑动时,试求:
如图,一个水平放置的导体框架,宽度L=2m,接有电阻R=4Ω,设匀强磁场和框架平面垂直,磁感应强度B=1T,方向如图.今有一导体棒ab跨放在框架上,并能无摩擦地沿框滑动,框架及导体ab电阻均不计,当ab受到一平行于导轨的水平外力F而以v=4m/s的速度向右匀速滑动时,试求: