题目内容
4.在平直公路上,自行车与同方向行驶的一汽车同时经过A点,它们的位移s(m)随时间t(s)的变化规律为:自行车:s1=6t;汽车:s2=10t-$\frac{1}{2}$t2.求:①经多长时间自行车追上汽车?
②自行车追上汽车时,汽车的速度多大?
③自行车追上汽车前它们的最大距离为多大?
分析 ①根据自行车和汽车的位移表达式得出初速度、加速度.根据位移关系求出追及的时间.
②根据速度时间公式求出自行车追上汽车时,汽车的速度.
③当两车速度相等时,相距最远,结合速度公式求出速度相等经历的时间,根据位移关系求出最大距离.
解答 解:①根据s1=s2得:6t=$10t-\frac{1}{2}{t}^{2}$,
代入数据解得:t=8s.
②根据${s}_{2}={v}_{0}t+\frac{1}{2}a{t}^{2}$=$10t-\frac{1}{2}{t}^{2}$知,汽车的初速度v0=10m/s,加速度a=-1m/s2,
则自行车追上汽车时,汽车的速度为:v=v0+at=10-1×8m/s=2m/s.
③自行车做匀速直线运动的速度为6m/s,
当两车速度相等时,相距最远,则有:t′=$\frac{v-{v}_{0}}{a}=\frac{6-10}{-1}s=4s$,
此时自行车的位移为:x1=vt′=6×4m=24m,
汽车的位移为:${x}_{2}=10×4-\frac{1}{2}×16m=32m$,
则自行车追上汽车前它们的最大距离为:△x=x2-x1=32-24m=8m.
答:①经8s时间自行车追上汽车;
②自行车追上汽车时,汽车的速度为2m/s;
③自行车追上汽车前它们的最大距离为8m.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式综合求解,知道速度相等时,两车有最大距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.用a、b、c、d表示四种单色光,若( )
①a、b从同种玻璃射向空气,a的临界角小于b的临界角;
②用b、c和d在相同条件下分别做单缝衍射实验,c的中央亮条纹间距最大
③b、d以相同入射角从空气射入玻璃三棱镜中,b光的偏折角大.
则可推断a、b、c、d可能分别是( )
①a、b从同种玻璃射向空气,a的临界角小于b的临界角;
②用b、c和d在相同条件下分别做单缝衍射实验,c的中央亮条纹间距最大
③b、d以相同入射角从空气射入玻璃三棱镜中,b光的偏折角大.
则可推断a、b、c、d可能分别是( )
| A. | 紫光、蓝光、红光、橙光 | B. | 蓝光、紫光、红光、橙光 | ||
| C. | 紫光、蓝光、橙光、红光 | D. | 紫光、橙光、红光、蓝光 |
7. 如图所示的容器,用活塞封闭着刚好饱和的一些水汽,测得水汽的压强为p,体积为V,当保持温度不变( )
如图所示的容器,用活塞封闭着刚好饱和的一些水汽,测得水汽的压强为p,体积为V,当保持温度不变( )
 如图所示的容器,用活塞封闭着刚好饱和的一些水汽,测得水汽的压强为p,体积为V,当保持温度不变( )
如图所示的容器,用活塞封闭着刚好饱和的一些水汽,测得水汽的压强为p,体积为V,当保持温度不变( )| A. | 上提活塞使水汽的体积增为2V时,水汽的压强变为$\frac{1}{2}$p | |
| B. | 下压活塞使水汽的体积减为$\frac{1}{2}$V时,水汽的压强增为2p | |
| C. | 下压活塞时,水汽的质量减小,水汽的密度减小 | |
| D. | 下压活塞时,水汽的质量和密度都变小 |
5.在冬季,剩有半瓶热水的暖水瓶经过一个夜晚后,第二天拔瓶口的软木塞时感觉很紧,不易拔出来,这主要是因为( )
| A. | 软木塞受潮膨胀 | B. | 瓶口因温度降低而收缩变小 | ||
| C. | 白天气温升高,大气压强变大 | D. | 瓶内气体因温度降低而压强减小 |
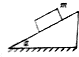 质量为m的物体,静止于一个倾角为α的斜面上,如图所示,如果已知物体所受重力和斜面对物体的弹力的合力方向平行于斜面向下,则这两个力的合力大小为mgsinα,斜面对物体的弹力大小为mgcosα,斜面对物体施加的摩擦力大小为mgsinα,方向平行于斜面向上.
质量为m的物体,静止于一个倾角为α的斜面上,如图所示,如果已知物体所受重力和斜面对物体的弹力的合力方向平行于斜面向下,则这两个力的合力大小为mgsinα,斜面对物体的弹力大小为mgcosα,斜面对物体施加的摩擦力大小为mgsinα,方向平行于斜面向上.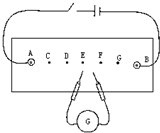 如图是描绘电场中等势线的实验装置,图中有7个等间距的点,其中A、B为金属电极,当电流从标有“+”号的接线柱流入灵敏电流计G时,其指针正向偏转,则当灵敏电流计指针不偏时,探针所接触的两点恰是等势点;当探针1接在F点时,探针2应在F点的正上方或者正下方的某个位置往右移,才能找到等势点.
如图是描绘电场中等势线的实验装置,图中有7个等间距的点,其中A、B为金属电极,当电流从标有“+”号的接线柱流入灵敏电流计G时,其指针正向偏转,则当灵敏电流计指针不偏时,探针所接触的两点恰是等势点;当探针1接在F点时,探针2应在F点的正上方或者正下方的某个位置往右移,才能找到等势点.