题目内容
20.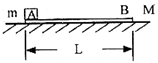 如图所示,长木板B质量为M,长L=1.0m,静止在光滑水平面上.一个质量为m的小木块(可视为质点)A,以水平速度v0=4m/s滑上B的左端,最后恰好停到木板B的右端.已知M=3m(取g=10m/s2).求:
如图所示,长木板B质量为M,长L=1.0m,静止在光滑水平面上.一个质量为m的小木块(可视为质点)A,以水平速度v0=4m/s滑上B的左端,最后恰好停到木板B的右端.已知M=3m(取g=10m/s2).求:(1)A、B最后的速度;
(2)木块A与木板B间的动摩擦因数.
分析 (1)根据动量守恒定律列方程求解;
(2)根据能量守恒定律列方程求摩擦因数;
解答 解:(1)铁块恰能滑到小车的右端,此时二者具有相同的速度v,规定向右为正方向,根据动量守恒定律:
mv0=(M+m)v
解得:v=$\frac{m{v}_{0}}{m+M}=\frac{m}{m+3m}×4$=1.0m/s
(2)根据能量守恒定律:μmgL=$\frac{1}{2}$mv02-$\frac{1}{2}$(M+m)v2
代入数据求得:μ=0.6
答:(1)A、B最后的速度是1m/s;(2)木块A与木板B间的动摩擦因数是0.6.
点评 本题考查了动量守恒定律和能量守恒定律的综合运用,第二问也可以用牛顿第二定律和运动学公式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图所示,质量为m的木块A放在地面上的质量为M的三角形斜劈B上,现用大小均为F、方向相反的力分别推A和B,它们均静止不动,则( )
如图所示,质量为m的木块A放在地面上的质量为M的三角形斜劈B上,现用大小均为F、方向相反的力分别推A和B,它们均静止不动,则( )
 如图所示,质量为m的木块A放在地面上的质量为M的三角形斜劈B上,现用大小均为F、方向相反的力分别推A和B,它们均静止不动,则( )
如图所示,质量为m的木块A放在地面上的质量为M的三角形斜劈B上,现用大小均为F、方向相反的力分别推A和B,它们均静止不动,则( )| A. | A与B之间一定存在弹力 | |
| B. | B与地面之间一定存在摩擦力 | |
| C. | B对A的支持力一定等于mg | |
| D. | 地面对B的支持力的大小一定等于Mg |
8.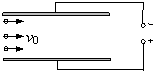 静电除尘装置的简化模型如图所示,重力可忽略的带负电尘埃,以速度v0垂直匀强电场飞入板间.为了使更多的尘埃打在板上,下列措施可行的是( )
静电除尘装置的简化模型如图所示,重力可忽略的带负电尘埃,以速度v0垂直匀强电场飞入板间.为了使更多的尘埃打在板上,下列措施可行的是( )
 静电除尘装置的简化模型如图所示,重力可忽略的带负电尘埃,以速度v0垂直匀强电场飞入板间.为了使更多的尘埃打在板上,下列措施可行的是( )
静电除尘装置的简化模型如图所示,重力可忽略的带负电尘埃,以速度v0垂直匀强电场飞入板间.为了使更多的尘埃打在板上,下列措施可行的是( )| A. | 只增大两极板间的宽度d | B. | 只增大两极板的长度L | ||
| C. | 只增大两极板间的电压U | D. | 只增大尘埃的速度v0 |
15.下列关于地球同步卫星的说法不正确的是( )
| A. | 它的周期与地球自转同步,但高度和速度可以选择 | |
| B. | 它的周期高度速度都是一定的 | |
| C. | 我国发射同步通讯卫星定点在北京上空 | |
| D. | 我国发射同步通讯卫星也定点在赤道上空 |
5. 2012年8月8日英国伦敦举行的奥运会上,刘翔虽然在110米跨栏中意外摔伤,但是他的奥运精神激励了中华儿女.他采用蹲踞式起跑,在发令枪响后,右脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设刘翔的质量为m,在起跑时前进的时间s内,重心升高h,获得的速度为v,克服阻力做功为W阻,则在此过程中( )
2012年8月8日英国伦敦举行的奥运会上,刘翔虽然在110米跨栏中意外摔伤,但是他的奥运精神激励了中华儿女.他采用蹲踞式起跑,在发令枪响后,右脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设刘翔的质量为m,在起跑时前进的时间s内,重心升高h,获得的速度为v,克服阻力做功为W阻,则在此过程中( )
 2012年8月8日英国伦敦举行的奥运会上,刘翔虽然在110米跨栏中意外摔伤,但是他的奥运精神激励了中华儿女.他采用蹲踞式起跑,在发令枪响后,右脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设刘翔的质量为m,在起跑时前进的时间s内,重心升高h,获得的速度为v,克服阻力做功为W阻,则在此过程中( )
2012年8月8日英国伦敦举行的奥运会上,刘翔虽然在110米跨栏中意外摔伤,但是他的奥运精神激励了中华儿女.他采用蹲踞式起跑,在发令枪响后,右脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设刘翔的质量为m,在起跑时前进的时间s内,重心升高h,获得的速度为v,克服阻力做功为W阻,则在此过程中( )| A. | 刘翔的机械能增加了$\frac{1}{2}$mv2 | |
| B. | 刘翔的重力做功为W重=mgh | |
| C. | 刘翔自身做功为W人=$\frac{1}{2}$mv2+mgh | |
| D. | 刘翔自身做功为W人=$\frac{1}{2}$mv2+mgh+W阻 |
9.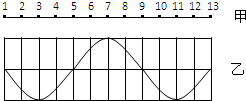 均匀介质中,各质点的平衡位置在同一直线上,相邻质点的距离均为s,如图甲所示.振动由质点1从平衡位置开始向右传播,质点1从平衡位置开始运动时的速度方向竖直向上,经过时间t,前13个质点第一次形成如图乙所示的波形.关于这列波的周期和波速有如下说法正确的是( )
均匀介质中,各质点的平衡位置在同一直线上,相邻质点的距离均为s,如图甲所示.振动由质点1从平衡位置开始向右传播,质点1从平衡位置开始运动时的速度方向竖直向上,经过时间t,前13个质点第一次形成如图乙所示的波形.关于这列波的周期和波速有如下说法正确的是( )
 均匀介质中,各质点的平衡位置在同一直线上,相邻质点的距离均为s,如图甲所示.振动由质点1从平衡位置开始向右传播,质点1从平衡位置开始运动时的速度方向竖直向上,经过时间t,前13个质点第一次形成如图乙所示的波形.关于这列波的周期和波速有如下说法正确的是( )
均匀介质中,各质点的平衡位置在同一直线上,相邻质点的距离均为s,如图甲所示.振动由质点1从平衡位置开始向右传播,质点1从平衡位置开始运动时的速度方向竖直向上,经过时间t,前13个质点第一次形成如图乙所示的波形.关于这列波的周期和波速有如下说法正确的是( )| A. | 周期是T=$\frac{2t}{3}$ | B. | 周期是T=$\frac{t}{2}$ | ||
| C. | 传播速度是v=$\frac{12s}{t}$ | D. | 传播速度是v=$\frac{16s}{t}$ |
10.质量为m的带正电的物体处于竖直向上的匀强电场中,已知带电物体所受静电力的大小为物体所受重力的$\frac{1}{4}$,现将物体从距地面高h处以一定初速度竖直下抛,物体以$\frac{g}{4}$的加速度竖直下落到地面(空气阻力恒定),则在物体的下落过程中( )
| A. | 物体的重力势能减少$\frac{1}{4}$mgh,电势能减少$\frac{1}{4}$mgh | |
| B. | 由物体与周围空气组成的系统的内能增加了$\frac{1}{2}$mgh | |
| C. | 物体的动能增加$\frac{1}{2}$mgh | |
| D. | 物体的机械能减少$\frac{1}{4}$mgh |
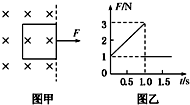 一正方形金属线框位于有界匀强磁场区域内,线框平面与磁场垂直,线框的右边紧贴着磁场边界,如图甲所示.t=0时刻对线框施加一水平向右的外力,让线框从静止开始做匀加速直线运动穿过磁场,外力F随时间t变化的图象如图乙所示.已知线框质量m=1kg、电阻R=1Ω,则磁场强度为2$\sqrt{2}$T.
一正方形金属线框位于有界匀强磁场区域内,线框平面与磁场垂直,线框的右边紧贴着磁场边界,如图甲所示.t=0时刻对线框施加一水平向右的外力,让线框从静止开始做匀加速直线运动穿过磁场,外力F随时间t变化的图象如图乙所示.已知线框质量m=1kg、电阻R=1Ω,则磁场强度为2$\sqrt{2}$T.