题目内容
(14分)如图所示,在坐标系xOy中,第一象限内充满着两个匀强磁场a和b,OP为分界线,倾角为37°,在区域a中,磁感应强度为2B,方向垂直于纸面向里;在区域b中,磁感应强度为B,方向垂直于纸面向外,P点坐标为(4L,3L).一质量为m、电荷量为q的带正电的粒子从P点沿y轴负方向射入区域b,经过一段时间后,粒子恰能经过原点O,不计粒子重力.(sin37°=0.6,cos37°=0.8)求:
(1)粒子从P点运动到O点的时间最少是多少?
(2)粒子运动的速度可能是多少?
(1) 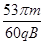 (2)
(2) 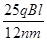 (n=1,2,3…)[
(n=1,2,3…)[
解析试题分析:(1)设粒子的入射速度为v,用Ra、Rb、Ta、Tb分别表示粒子在磁场a区和b区运动的轨道半径和周期
则有: Ra=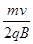 Rb=
Rb=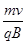 Ta=
Ta=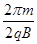 =
=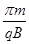 Tb=
Tb=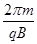
粒子先从b区运动,再进入a区运动,然后从O点射出时,粒子从P运动到O点所用时间最短.如图所示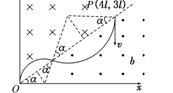
tanα=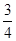 得:α=37°
得:α=37°
粒子在b区和a区运动的时间分别为:tb=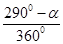 Tb ta=
Tb ta=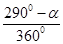 Ta
Ta
故从P点运动到O点所用最短时间为: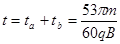
(2)由题意及图可知: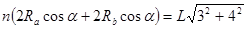
解得: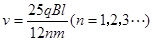
考点:带电粒子在磁场中的运动

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
如图所示,在线圈上端放置一盛有冷水的金属杯,现接通交流电源,过了几分钟,杯内的水沸腾起来。若要缩短上述加热时间,下列措施可行的有( )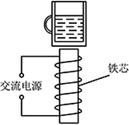
| A.增加线圈的匝数 | B.提高交流电源的频率 |
| C.将金属杯换为瓷杯 | D.取走线圈中的铁芯 |
 OC,E点在D点正下方,位于x轴上,重力加速度为g。则:
OC,E点在D点正下方,位于x轴上,重力加速度为g。则:
 时刻粒子由C点进入第一象限,且恰好也能通过同一水平线上的D点,速度方向仍然水平。若粒子在第一象限中运动的周期与磁场变化周期相同,求交变磁场变化的周期;
时刻粒子由C点进入第一象限,且恰好也能通过同一水平线上的D点,速度方向仍然水平。若粒子在第一象限中运动的周期与磁场变化周期相同,求交变磁场变化的周期;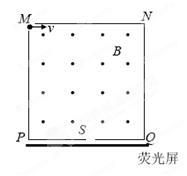
 )。
)。
 大小、方向如何?
大小、方向如何?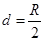 的电子在圆形磁场中运动了多长时间?
的电子在圆形磁场中运动了多长时间? m,P、Q分别是ac、bc的中点。一带正电的粒子(不计重力)从ab边中点O沿Oc方向以速度
m,P、Q分别是ac、bc的中点。一带正电的粒子(不计重力)从ab边中点O沿Oc方向以速度 射入,带电粒子恰好做匀速直线运动,从c点射出。
射入,带电粒子恰好做匀速直线运动,从c点射出。

 延长线的夹角为30°.粒子在这过程中只受磁场力的作用。
延长线的夹角为30°.粒子在这过程中只受磁场力的作用。
