题目内容
 重150N的光滑球A悬空靠在墙和木板B之间,木板B的重力为1500N,且静止在水平地板上,如图所示,求:
重150N的光滑球A悬空靠在墙和木板B之间,木板B的重力为1500N,且静止在水平地板上,如图所示,求:(1)墙和木块B所受压力各为多少?
(2)水平地板所受的压力和木块B所受的摩擦力各为多少?
分析:(1)先对小球A受力分析,然后根据共点力平衡条件列式求解球受到的弹力,最后根据牛顿第三定律求解其反作用力;
(2)对木块B受力分析,然后根据平衡条件列式求解 摩擦力和地面的支持力,最后根据牛顿第三定律求解其对地面的压力.
(2)对木块B受力分析,然后根据平衡条件列式求解 摩擦力和地面的支持力,最后根据牛顿第三定律求解其对地面的压力.
解答:解:(1)小球A和木块B受力分析如图所示,用N1、N2、N3、N1分别表示木块对A的弹力、墙壁对A的支持力、地面对木块的支持力和小球对木块的弹力.
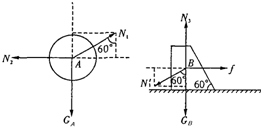
对小球A,根据共点力平衡条件,有:
N1sin60°=N2 ①
N1cos60°=GA ②
由以上两式得N2=150
N,N1=300N.
根据牛顿第三定律,墙壁受到的压力N′2=150
N,木块B所受到的压力N1′=300N.
(2)对木块B受力分析,如上图所示,根据共点力平衡条件,有:
N1′cos60°+GB=N3 ③
N1′sin60°=f ④
把N1′=300N代入③④
可得:N3=1650N,f=150
N.
根据作用力和反作用力的关系,水平地板所受的压力N'3=1650N.
答:(1)墙所受压力为150
N,木块B所受压力为300N;
(2)水平地板所受的压力为1650N,木块B所受的摩擦力为150
N.

对小球A,根据共点力平衡条件,有:
N1sin60°=N2 ①
N1cos60°=GA ②
由以上两式得N2=150
| 3 |
根据牛顿第三定律,墙壁受到的压力N′2=150
| 3 |
(2)对木块B受力分析,如上图所示,根据共点力平衡条件,有:
N1′cos60°+GB=N3 ③
N1′sin60°=f ④
把N1′=300N代入③④
可得:N3=1650N,f=150
| 3 |
根据作用力和反作用力的关系,水平地板所受的压力N'3=1650N.
答:(1)墙所受压力为150
| 3 |
(2)水平地板所受的压力为1650N,木块B所受的摩擦力为150
| 3 |
点评:本题关键对两个物体受力分析后,运用共点力平衡条件列式求解未知力,最后结合牛顿第三定律求解反作用力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 重150N的光滑球A悬空靠在墙和木块B之间,木块B的重力为1500N,且静止在水平地板上,如图所示,则下列判断正确的是( )
重150N的光滑球A悬空靠在墙和木块B之间,木块B的重力为1500N,且静止在水平地板上,如图所示,则下列判断正确的是( )| A、墙所受压力的大小为150N | ||
| B、木块A对木块B压力的大小为150N | ||
| C、水平地板所受的压力为1500N | ||
D、木块B所受摩擦力大小为150
|
 重150N的光滑球A悬空靠在竖直墙和三角形木块B之间,木块B的重力为1500N,且静止在水平地面上,如图所示,则( )
重150N的光滑球A悬空靠在竖直墙和三角形木块B之间,木块B的重力为1500N,且静止在水平地面上,如图所示,则( )
