题目内容
如图所示,光滑水平面AB与竖直面的半圆形导轨在B点相连接,导轨半径为R,一个质量为m的静止的木块在A处压缩弹簧,释放后,木块获得向右的初速度,当它经过B点进入半圆形导轨瞬间对导轨的压力是其重力的7倍,之后向上运动恰能通过轨道最高点C,试求:
(1)木块到达B处时的速度大小;
(2)木块释放前,弹簧所具有的弹性势能;
(3)木块从B到C过程中克服摩擦力所做的功。
(1)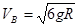 (2)
(2)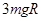 (3)
(3)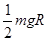
解析试题分析:(1)根据牛顿第二定律可得: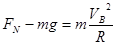 解得
解得 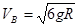 (3分)
(3分)
(2)弹簧的弹性势能全部转化为物体的动能,故有: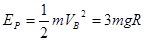 (3分)
(3分)
(3)在C点: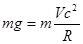
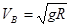 (3分)
(3分)
B→C过程中: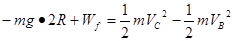 (3分)
(3分)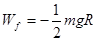 克服阻力做功
克服阻力做功 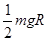 (2分)
(2分)
考点:动能定理的应用;牛顿第二定律;
点评:对于圆周运动的受力问题,我们要找出向心力的来源.动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用计算机辅助实验系统做验证牛顿第三定律的实验,点击实验菜单中“力的相互作用”。如图(a)所示,把两个力探头的挂钩钩在一起,向相反方向拉动,观察显示器屏幕上出现的结果[图(b)]。分析两个力传感器的相互作用力随时间变化的曲线,以下结论错误的是: 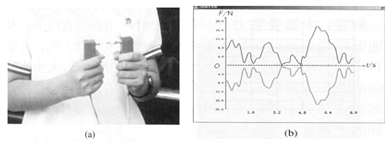
| A.作用力与反作用力大小时刻相等 |
| B.作用力与反作用力作用在同一物体上 |
| C.作用力与反作用力大小同时变化 |
| D.作用力与反作用力方向相反 |
如图所示,将一个质量为m的球固定在弹性杆AB的上端,今用测力计沿水平方向缓慢拉球,使杆发生弯曲,在测力计的示数逐渐增大的过程中,AB杆对球的弹力方向为( )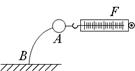
| A.始终水平向左 |
| B.始终斜向左上方,且方向不变 |
| C.斜向左上方,与竖直方向的夹角逐渐增大 |
| D.斜向左下方,与竖直方向的夹角逐渐增大 |
“蹦极”是一项非常刺激的体育运动.某人身系弹性绳自高空P点自由下落,图中a点是弹性绳的原长位置,c是人所到达的最低点,b是人静止悬吊着时的平衡位置,人在从P点下落到最低点c点的过程中( )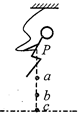
| A.在 Pa 段做自由落体运动,处于完全失重状态 |
| B.ab 段绳的拉力小于人的重力,人处于失重状态 |
| C.bc 段绳的拉力大于人的重力,人处于超重状态 |
| D.c点,人的速度为零,处于平衡状态 |