题目内容
如图 所示,一质量为500kg的木箱放在质量为2000kg的平板车的后端,木箱到驾驶室的距离L=1.6m,已知木箱与车板间的动摩擦因数μ=0.484,平板车在运动过程中所受阻力是车和箱总重的0.20倍,平板车以v=22.0m/s恒定速度行驶,突然驾驶员刹车做
所示,一质量为500kg的木箱放在质量为2000kg的平板车的后端,木箱到驾驶室的距离L=1.6m,已知木箱与车板间的动摩擦因数μ=0.484,平板车在运动过程中所受阻力是车和箱总重的0.20倍,平板车以v=22.0m/s恒定速度行驶,突然驾驶员刹车做 匀减速运动,为使木箱不撞击驾驶室,g取10m/s2,试求:
匀减速运动,为使木箱不撞击驾驶室,g取10m/s2,试求:
(1)从刹车开始到平板车完全停止至少要经过多长时间?
(2)驾驶员刹车时的制动力不能超过多大?
 所示,一质量为500kg的木箱放在质量为2000kg的平板车的后端,木箱到驾驶室的距离L=1.6m,已知木箱与车板间的动摩擦因数μ=0.484,平板车在运动过程中所受阻力是车和箱总重的0.20倍,平板车以v=22.0m/s恒定速度行驶,突然驾驶员刹车做
所示,一质量为500kg的木箱放在质量为2000kg的平板车的后端,木箱到驾驶室的距离L=1.6m,已知木箱与车板间的动摩擦因数μ=0.484,平板车在运动过程中所受阻力是车和箱总重的0.20倍,平板车以v=22.0m/s恒定速度行驶,突然驾驶员刹车做 匀减速运动,为使木箱不撞击驾驶室,g取10m/s2,试求:
匀减速运动,为使木箱不撞击驾驶室,g取10m/s2,试求:(1)从刹车开始到平板车完全停止至少要经过多长时间?
(2)驾驶员刹车时的制动力不能超过多大?

(1)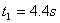
(2)F=7420N
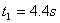
(2)F=7420N
解:(1)刹车时间越短刹车加速度越大,箱会相对板车滑动。设刹车后,平板车的加速度为a1,到停止时历时t1,车行的位移s1,则有: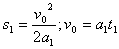
设刹车后,箱的加速度为a2,箱滑行的位移s2,则有: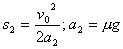
为不使箱撞驾驶室,应有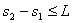 ,联立以上各式解
,联立以上各式解 得:
得: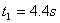
(2)对平板车,设制动力为F,则依牛顿第二定律:
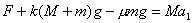
当t 最短时,a1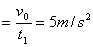
最大制动力F=7420N
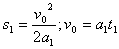
设刹车后,箱的加速度为a2,箱滑行的位移s2,则有:
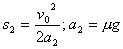
为不使箱撞驾驶室,应有
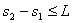 ,联立以上各式解
,联立以上各式解 得:
得: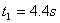
(2)对平板车,设制动力为F,则依牛顿第二定律:
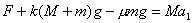
当t 最短时,a1
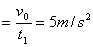
最大制动力F=7420N

练习册系列答案
相关题目

 的物体,以水平速度
的物体,以水平速度 滑上静止在光滑水平面上的平板小车,如图所示,小车的质量
滑上静止在光滑水平面上的平板小车,如图所示,小车的质量 ,物体在平板小车上相对小车滑行了一段距离
,物体在平板小车上相对小车滑行了一段距离 后不再滑动,
后不再滑动, 取
取 ,求:
,求: =0.01,物体仍以
=0.01,物体仍以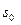 与
与 的大小。要求有根据。(车做够长)
的大小。要求有根据。(车做够长)
 mg与速度反向
mg与速度反向