题目内容
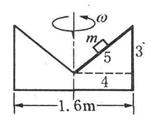
(14分)在直径1.6m的圆柱体一端截出一圆锥,如下图所示,在看到剖面上,三角形的三边之比为3:4:5, 圆柱体可绕其中心对称轴匀速旋转。将一小木块放置在斜面的中点,它与斜面间动摩擦力因素为0.25,若小木块保持在此位置不动,则圆柱体旋转的角速度应为多大.
( ;g取10m/s2)
;g取10m/s2)
【答案】
3.2rad/s≤ω≤5.4rad/s
【解析】
试题分析:当圆柱体旋转角速度最小为ωmin时,木块有沿斜面向下滑动趋势,木块受最大静摩擦力f的方向沿斜面向上。木块受重力mg、斜面支持力N和静摩擦f,如图所示。
木块在水平面内作匀速圆周运动,向心加速度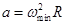 ,R=0.4m。
,R=0.4m。

根据牛顿第二定律得
水平方向: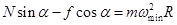 ①
①
竖直方向: Ncosα+fsinα=mg ②
又 f=μN ③
联立①、②、③解得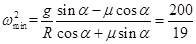

当圆柱体旋转角速度最大为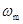 时,木块有沿斜面向上滑动趋势,木块受最大静摩擦力f的方向沿斜面向下。木块还受重力mg和斜面支持力N′作用,如图所示。木块加速度
时,木块有沿斜面向上滑动趋势,木块受最大静摩擦力f的方向沿斜面向下。木块还受重力mg和斜面支持力N′作用,如图所示。木块加速度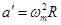 。 由牛顿第二定律得
。 由牛顿第二定律得

水平方向: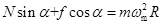 ④
④
竖直方向: Ncosα-fsinα=mg ⑤
又 f′=μN′ ⑥
联立④、⑤、⑥解得


圆柱体旋转的角速度ω应为3.2rad/s≤ω≤5.4rad/s
考点:圆周运动
点评:本题考查了圆周运动中常见的临界问题,也是该类问题中比较常见典型的问题,要找到问题突破口,本题主要是因为静摩擦力的方向不确定造成。

练习册系列答案
相关题目

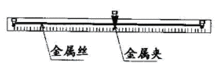

 (4)他们使用螺旋测微器测量金属丝的直径,示数如图所示。金属丝的直径是______。图中图线的斜率、电源电动势和金属丝横截面积的乘积代表的物理量是________,其数值和单位为___________(保留三位有效数字)。
(4)他们使用螺旋测微器测量金属丝的直径,示数如图所示。金属丝的直径是______。图中图线的斜率、电源电动势和金属丝横截面积的乘积代表的物理量是________,其数值和单位为___________(保留三位有效数字)。 
 ;g取10m/s2)
;g取10m/s2)