题目内容
(12分).如图所示,水平面上某点固定一轻质弹簧,A点左侧的水平面光滑,右侧水平面粗糙,在A点右侧5m远处(B点)竖直放置一半圆形光滑轨道,轨道半径R=0.4m,连接处平滑。现将一质量m=0.1kg的小滑块放在弹簧的右端(不拴接),用力向左推滑块而压缩弹簧,使弹簧具有的弹性势能为2J,放手后,滑块被向右弹出,它与A点右侧水平面的动摩擦因数μ=0.2,取g =10m/s2,求:
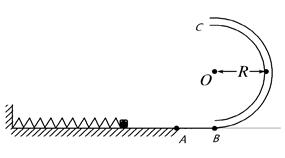
(1)滑块运动到半圆形轨道最低点B处时对轨道的压力;
(2)改变半圆形轨道的位置(左右平移),使得被弹出的滑块到达半圆形轨道最高点C处时对轨道的压力大小等于滑块的重力,问AB之间的距离应调整为多少?
(1)6N,方向竖直向下(2)x2 =" 6" m
【解析】
试题分析:(1)从小滑块被释放到到达B点的过程中,据动能定理有
W弹 - μmg·x = 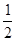 mvC2 (1分)
mvC2 (1分)
滑块在圆周轨道B点处,有 (1分)
(1分)
把W弹 = ΔEP ="2" J等数据代入,解得FN =" 6" N (1分)
由牛顿第三定律可知,滑块对轨道的压力大小为6N,方向竖直向下。 (1分)
(2)在圆周最高点C处,滑块对轨道的压力等于其重力,包含了两种情况:
第一,当压力方向向上(滑块受到的支持力向下)时,
在C点处,有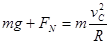 (1分)
(1分)
整个过程有W弹 -
μmg·x1 = 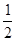 mvC2 (1分)
mvC2 (1分)
把FN = mg代入得x1 =" 4" m (1分)
第二,当压力方向向下(滑块受到的支持力向上)时,同理可解得x2 =" 6" m (3分)
考点:考查动能定理和圆周运动的结合
点评:本题难度中等,涉及到能量转化问题,要从能量守恒角度考虑,从开始到运动到B点,弹簧的弹性势能转化为克服摩擦力做功和物块的动能,在B点由半径方向上的合力提供向心力,熟练掌握动能定理是本题求解的关键

 (2005?江苏)如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和 P之间接有阻值为R的定值电阻,导体棒ab长l=0.5m,其电阻为r,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.
(2005?江苏)如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和 P之间接有阻值为R的定值电阻,导体棒ab长l=0.5m,其电阻为r,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动. 如图所示,水平面上复印机纸盒里放一叠共计10张复印纸,每一张纸的质量均为m.用一摩擦轮以竖直向下的力F压第1张纸,并以一定的角速度逆时针转动摩擦轮,确保摩擦轮与第1张纸之间.第1张纸与第2张纸之间均有相对滑动.设最大静摩擦力与滑动摩擦力相同,摩擦轮与第1张纸之间的动摩擦因数为μ1,纸张间的动摩擦因数均为μ2,且有μ1>μ2.则下列说法正确的是( )
如图所示,水平面上复印机纸盒里放一叠共计10张复印纸,每一张纸的质量均为m.用一摩擦轮以竖直向下的力F压第1张纸,并以一定的角速度逆时针转动摩擦轮,确保摩擦轮与第1张纸之间.第1张纸与第2张纸之间均有相对滑动.设最大静摩擦力与滑动摩擦力相同,摩擦轮与第1张纸之间的动摩擦因数为μ1,纸张间的动摩擦因数均为μ2,且有μ1>μ2.则下列说法正确的是( ) 如图所示,水平面上有一块木板,质量M=4.0kg,它与水平面间的动摩擦因数μ1=0.10.在木板的最左端有一个小滑块(可视为质点),质量m=2.0kg.小滑块与木板之间的动摩擦因数μ2=0.50.开始时它们都处于静止状态.某时刻起对小滑块施加一个水平向右的恒力F=18N,此后小滑块将相对木板滑动,1.0s后撤去该力.
如图所示,水平面上有一块木板,质量M=4.0kg,它与水平面间的动摩擦因数μ1=0.10.在木板的最左端有一个小滑块(可视为质点),质量m=2.0kg.小滑块与木板之间的动摩擦因数μ2=0.50.开始时它们都处于静止状态.某时刻起对小滑块施加一个水平向右的恒力F=18N,此后小滑块将相对木板滑动,1.0s后撤去该力. 如图所示,水平面上有电阻不计的U形光滑导轨NMPQ,它们之间的宽度为L,M和P之间接入电动势为E的电源(不计内阻).现垂直于导轨搁一根质量为m、电阻为R的金属棒ab,并加一个范围较大的匀强磁场,磁感应强度为B,方向与水平面的夹角为θ且指向右方.若棒ab始终与导轨接触良好,则棒ab所受的支持力和在水平方向上的加速度分别是多少?
如图所示,水平面上有电阻不计的U形光滑导轨NMPQ,它们之间的宽度为L,M和P之间接入电动势为E的电源(不计内阻).现垂直于导轨搁一根质量为m、电阻为R的金属棒ab,并加一个范围较大的匀强磁场,磁感应强度为B,方向与水平面的夹角为θ且指向右方.若棒ab始终与导轨接触良好,则棒ab所受的支持力和在水平方向上的加速度分别是多少? 如图所示,水平面上两根足够长且光滑的金属导轨平行固定放置,间距为L=0.5m,一端通过导线与阻值为R=0.5Ω的电阻连接;导轨上放一金属杆ab,金属杆与导轨的电阻不计;匀强磁场的磁感强度B=1T,方向竖直向下.现用与导轨平行的恒定外力F=5N作用在金属杆上,ab杆最终将做匀速运动.
如图所示,水平面上两根足够长且光滑的金属导轨平行固定放置,间距为L=0.5m,一端通过导线与阻值为R=0.5Ω的电阻连接;导轨上放一金属杆ab,金属杆与导轨的电阻不计;匀强磁场的磁感强度B=1T,方向竖直向下.现用与导轨平行的恒定外力F=5N作用在金属杆上,ab杆最终将做匀速运动.