题目内容
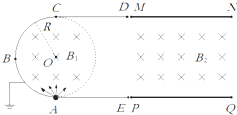 (2013?重庆二模)为了获得一束速度大小确定且方向平行的电子流,某人设计了一种实验装置,其截面图如图所示.其中EABCD为一接地的金属外壳.在A处有一粒子源,可以同时向平行于纸面的各个方向射出大量的速率不等的电子.忽略电子间的相互作用力,这些电子进入一垂直于纸面向里的圆形区域匀强磁场后,仅有一部分能进入右侧的速度选择器MNPQ.已知圆形磁场半径为R;速度选择器的MN和PQ板都足够长,板间电场强度为E(图中未画出电场线),匀强磁场垂直于纸面向里大小为B2,电子的电荷量大小为e,质量为m.调节圆形区域磁场的磁感应强度B1的大小,直到有电子从速度选择器右侧射出.求:
(2013?重庆二模)为了获得一束速度大小确定且方向平行的电子流,某人设计了一种实验装置,其截面图如图所示.其中EABCD为一接地的金属外壳.在A处有一粒子源,可以同时向平行于纸面的各个方向射出大量的速率不等的电子.忽略电子间的相互作用力,这些电子进入一垂直于纸面向里的圆形区域匀强磁场后,仅有一部分能进入右侧的速度选择器MNPQ.已知圆形磁场半径为R;速度选择器的MN和PQ板都足够长,板间电场强度为E(图中未画出电场线),匀强磁场垂直于纸面向里大小为B2,电子的电荷量大小为e,质量为m.调节圆形区域磁场的磁感应强度B1的大小,直到有电子从速度选择器右侧射出.求:(1)速度选择器的MN板带正电还是负电?能从速度选择器右侧射出的电子的速度v0大小、方向如何?
(2)是否所有从粒子源A处射出并进入磁场的速度大小为(1)问中v0的电子,最终都能从速度选择器右侧射出?若能,请简要证明,并求出圆形磁场的磁感应强度B1的大小;若不能,请说明理由.(不考虑电子“擦”到金属板的情形以及金属板附近的边界效应)
(3)在最终能通过速度选择器的电子中,从圆形区域磁场出射时距AE为d=
| R | 2 |
分析:(1)电子从左侧进入,能从右侧射出的电子,所受洛伦兹力与电场力平衡,根据洛伦兹力的方向可以判定电场力的方向,从而得到极板的带电情况;
(2)当粒子进入磁场中做圆周运动的半径r=R时,根据几何关系可以证明粒子运动轨迹确定粒子在磁场中偏转角度与水平方向的夹角相等,即只要以v0进入磁场后都能以水平方向速度进入速度选择器,故根据半径关系可以求出B1的大小;
(3)作出粒子的运动轨迹,根据几何关系求出粒子在圆形磁场中做圆周运动转过的圆心角,根据t=
T求时间即可.
(2)当粒子进入磁场中做圆周运动的半径r=R时,根据几何关系可以证明粒子运动轨迹确定粒子在磁场中偏转角度与水平方向的夹角相等,即只要以v0进入磁场后都能以水平方向速度进入速度选择器,故根据半径关系可以求出B1的大小;
(3)作出粒子的运动轨迹,根据几何关系求出粒子在圆形磁场中做圆周运动转过的圆心角,根据t=
| θ |
| 2π |
解答:解:(1)能通过速度选择器的电子都满足电场力和洛伦兹力平衡的粒子才可以通过速度选择器,即能过速度选择器的电子具有水平向右的速度,根据左手定则可以判定电子所受洛伦力方向竖直向下,故电场力方向竖直向上,从而确定MN板带正电.
在速度选择器中:
eE=ev0B2
∴v0=
,方向平行于MN向右
(2)所有以速度v0进入磁场的电子,都能从速度选择器右侧射出
如图为从圆形磁场在侧圆弧上任意一点F向右射出速度大小为v0的电子运动轨迹
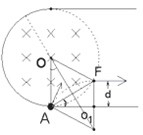
由几何知识易证:∠O1FA=∠OAF=∠OFA
故平行四边形AOFO1 为菱形,O1F=OF
即所有向右平行于MN射出磁场的电子,做圆周运动的半径都等于圆形磁场区域的半径.只要速度大小为v0,其圆周运动的半径就等于磁场区域半径,都能向右射出磁场,并最终通过速度选择器.
r=R
r=
∴B1=
=
(3)如图,
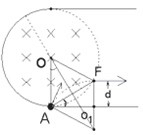
由几何关系:O1F=R,d=
可得:AF=R
即粒子在圆形磁场中偏转的圆心角∠AO1F=60°
粒子在B1的磁场中做圆周运动的周期T=
=
=
粒子在圆形磁场中运动的时间t=
T=
T=
答:(1)速度选择器的MN板带正电,能从速度选择器右侧射出的电子的速度v0大小为v0=
方向水平向右.
(2)若圆形区域的磁场满足B1=
=
,则所有从粒子源A处射出并进入磁场的速度大小为(1)问中v0的电子,都最终都能从速度选择器右侧射出.
(3)在最终能通过速度选择器的电子中,从圆形区域磁场出射时距AE为d=
的电子在圆形磁场中运动了的时间为:
.
在速度选择器中:
eE=ev0B2
∴v0=
| E |
| B2 |
(2)所有以速度v0进入磁场的电子,都能从速度选择器右侧射出
如图为从圆形磁场在侧圆弧上任意一点F向右射出速度大小为v0的电子运动轨迹

由几何知识易证:∠O1FA=∠OAF=∠OFA
故平行四边形AOFO1 为菱形,O1F=OF
即所有向右平行于MN射出磁场的电子,做圆周运动的半径都等于圆形磁场区域的半径.只要速度大小为v0,其圆周运动的半径就等于磁场区域半径,都能向右射出磁场,并最终通过速度选择器.
r=R
r=
| mv |
| eB1 |
∴B1=
| mv |
| eR |
| mE |
| eRB2 |
(3)如图,

由几何关系:O1F=R,d=
| R |
| 2 |
可得:AF=R
即粒子在圆形磁场中偏转的圆心角∠AO1F=60°
粒子在B1的磁场中做圆周运动的周期T=
| 2πm |
| eB1 |
| 2πm | ||
e
|
| 2πRB2 |
| E |
粒子在圆形磁场中运动的时间t=
| θ |
| 2π |
| 1 |
| 6 |
| πRB2 |
| 3E |
答:(1)速度选择器的MN板带正电,能从速度选择器右侧射出的电子的速度v0大小为v0=
| E |
| B2 |
(2)若圆形区域的磁场满足B1=
| mv |
| eR |
| mE |
| eRB2 |
(3)在最终能通过速度选择器的电子中,从圆形区域磁场出射时距AE为d=
| R |
| 2 |
| πRB2 |
| 3E |
点评:带电粒子在磁场中的运动,重点要把握好“找圆心、求半径”,注意画出草图,同时利用好几何关系去分析粒子的运动过程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013?重庆二模)一带电小球在电场中仅在电场力作用下,从A点运动到B点,速度大小随时间变化的图象如图所示,t1、t2分别是带电小球在A、B两点对应的时刻,则下列说法中正确的有( )
(2013?重庆二模)一带电小球在电场中仅在电场力作用下,从A点运动到B点,速度大小随时间变化的图象如图所示,t1、t2分别是带电小球在A、B两点对应的时刻,则下列说法中正确的有( ) (2013?重庆二模)如图所示,空间某区域中有一匀强磁场,磁感应强度方向水平,且垂直于纸面向里,磁场上边界b和下边界d水平.在竖直面内有一矩形金属线框,线框上下边的距离很短,磁场上下边界之间的距离大于a、b之间的距离.线框从水平面a开始下落,当线框下边刚通过水平面b、c、d时,线框所受到的磁场力的大小分别为Fb、Fc和Fd,则( )
(2013?重庆二模)如图所示,空间某区域中有一匀强磁场,磁感应强度方向水平,且垂直于纸面向里,磁场上边界b和下边界d水平.在竖直面内有一矩形金属线框,线框上下边的距离很短,磁场上下边界之间的距离大于a、b之间的距离.线框从水平面a开始下落,当线框下边刚通过水平面b、c、d时,线框所受到的磁场力的大小分别为Fb、Fc和Fd,则( ) (2013?重庆二模)如图所示,一个半径为R的金属圆环被支架M固定在水平地面上.可视为质点的小球A、B用不可伸长的细软轻线连接,跨过圆环,A的质量为B的两倍.当B位于地面时,A恰好处于圆环的水平直径右端且离地面高为h.现将A由静止释放,B相对地面上升的最大高度是(A触地后,B上升过程中绳一直处于松弛状态)( )
(2013?重庆二模)如图所示,一个半径为R的金属圆环被支架M固定在水平地面上.可视为质点的小球A、B用不可伸长的细软轻线连接,跨过圆环,A的质量为B的两倍.当B位于地面时,A恰好处于圆环的水平直径右端且离地面高为h.现将A由静止释放,B相对地面上升的最大高度是(A触地后,B上升过程中绳一直处于松弛状态)( )