题目内容
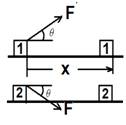
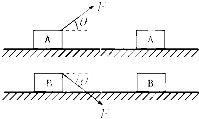
如图所示,两个物体中间用一个不计质量的轻杆相连.A、B两物体质量分别为m1、m2,它们和斜面间的滑动摩擦系数分别为μ1、μ2.当它们在斜面上加速下滑时,关于杆的受力情况,以下说法不正确的是( )
A.若μ1=μ2,则杆一定受到压力
B.若μ1=μ2,m1<m2,则杆受到压力
C.若μ1<μ2,m1>m2,则杆受到拉力
D.只要μ1=μ2,则杆的两端既不受拉力也没有压力
【答案】分析:假设杆无弹力,根据牛顿第二定律分别求解出A和B的加速度,比较大小,然后判断AB的相对运动趋势,再判断AB间弹力的方向.
解答:解:假设杆无弹力,滑块受重力、支持力和滑动摩擦力,根据牛顿第二定律,有:
m1gsinθ-μ1gcosθ=ma1
解得:a1=g(sinθ-μ1cosθ);
同理a2=gsinθ-μ2cosθ;
A、若μ1=μ2,则a1=a2,两个滑块加速度相同,说明无相对滑动趋势,故杆无弹力,故A错误;
B、若μ1=μ2,m1<m2,则a1=a2,两个滑块加速度相同,说明无相对滑动趋势,故杆无弹力,故B正确;
C、若μ1<μ2,m1>m2,则a1>a2,两个滑块有远离趋势,故杆有拉力,故C错误;
D、只要μ1=μ2,则a1=a2,两个滑块加速度相同,说明无相对滑动趋势,故杆无弹力,故D正确;
故选BD.
点评:本题关键先假设杆无弹力,然后根据牛顿第二定律求解出两个加速度并判断两个滑块的相对运动趋势,不难.
解答:解:假设杆无弹力,滑块受重力、支持力和滑动摩擦力,根据牛顿第二定律,有:
m1gsinθ-μ1gcosθ=ma1
解得:a1=g(sinθ-μ1cosθ);
同理a2=gsinθ-μ2cosθ;
A、若μ1=μ2,则a1=a2,两个滑块加速度相同,说明无相对滑动趋势,故杆无弹力,故A错误;
B、若μ1=μ2,m1<m2,则a1=a2,两个滑块加速度相同,说明无相对滑动趋势,故杆无弹力,故B正确;
C、若μ1<μ2,m1>m2,则a1>a2,两个滑块有远离趋势,故杆有拉力,故C错误;
D、只要μ1=μ2,则a1=a2,两个滑块加速度相同,说明无相对滑动趋势,故杆无弹力,故D正确;
故选BD.
点评:本题关键先假设杆无弹力,然后根据牛顿第二定律求解出两个加速度并判断两个滑块的相对运动趋势,不难.

练习册系列答案
相关题目
 A、B两个相同的物体,静止在动摩擦因数相同的地面上,现对两物体施加等大的恒力F,拉力的方向如图所示,两个物体在恒力的作用下发生了相同的位移,在此过程中.则下列说法正确的是( )
A、B两个相同的物体,静止在动摩擦因数相同的地面上,现对两物体施加等大的恒力F,拉力的方向如图所示,两个物体在恒力的作用下发生了相同的位移,在此过程中.则下列说法正确的是( )| A、拉力F对两物体做功相同 | B、拉力F对两物体做功的平均功率相同 | C、拉力F对物体1做功较大 | D、拉力F对物体1做功的平均功率较大 |
 如图所示,两个物体A和B由同一地点出发沿同一直线向同一方向运动的v-t图象运动过程中,A、B的运动情况为( )
如图所示,两个物体A和B由同一地点出发沿同一直线向同一方向运动的v-t图象运动过程中,A、B的运动情况为( ) 如图所示为两个物体A和B在同一直线上沿同一方向同时做匀加速运动的v-t图线.已知在第3s末两个物体在途中相遇,则下列说法正确的是( )
如图所示为两个物体A和B在同一直线上沿同一方向同时做匀加速运动的v-t图线.已知在第3s末两个物体在途中相遇,则下列说法正确的是( )