题目内容
【题目】如图所示为赛车场的一个“梨形”赛道，两个弯道分别为半径R=90m的大圆弧和r=40m的小圆弧，直道与弯道相切。大、小圆弧圆心O'、O距离L=100m。赛车沿弯道路线行驶时，路面对轮胎的最大径向静摩擦力是赛车重力的2．25倍，假设赛车在直道上做匀变速直线运动，在弯道上做匀速圆周运动，要使赛车不打滑，绕赛道一圈时间最短。（发动机功率足够大，重力加速度g=10m/s2，
=3．14）。
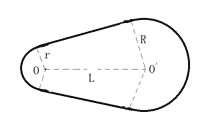
求：（1）在两个弯道上的最大速度分别是多少？
（2）应从什么位置开始加速，加速度是多大？
（3）完成一圈的最短时间是多少？
【答案】（1）30m/s 45m/s （2）6．50 m/s2（3）15．79s
【解析】试题分析： （1）在弯道上做匀速圆周运动时，径向摩擦力提供向心力，根据牛顿定律
，（2分）
在小弯道上的最大速度：
，（1分）
在大圆弧弯道上的速率为
（1分）
（2）当弯道半径一定 时，在弯道上的最大速度是一定的，且在大弯道上的最大速度大于小湾道上的最大速度，故要想时间最短，故可在绕过小圆弧弯道后加速，直道的长度为
，（2分）
由运动学公式
带入数据可得加速度大小为
，（1分）
由几何关系可知，小圆弧对应的圆心角
，大圆弧对应的圆心角
；所以小圆弧轨道的长度为
，所以小圆弧轨道的长度为
通过小圆弧弯道的时间为
， （1分）
通过大圆弧时间
S（1分）
直线运动时间为
，由运动学公式:
解得
（1分）
总时间
=15．79s（2分）
练习册系列答案
相关题目
