题目内容
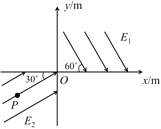
【题目】如图所示，在平面直角坐标系xOy的第一、三象限分布存在匀强电场E1、E2，电场E1的场强大小为
，方向与x轴负方向成60°斜向下，电场E2的场强大小未知，方向与x轴正方向成30°角斜向上，比荷为1.0×105 C/kg的带正电粒子a从第三象限的P点由静止释放，粒子沿PO做匀加速直线运动，到达O点的速度为104 m/s，不计粒子的重力。
(1)求P、O两点间的电势差；
(2)粒子a插进入电场E1时，在电场E1某位置由静止释放另外一个完全相同的带电粒子b，使两粒子在离开电场前相遇，若相遇时所需时间最长，求在电场E1中由静止释放的带电粒子b的初始位置坐标。
【答案】(1) 
(2) 
【解析】
(1)带电粒子a由P点运动到O点，根据动能定理有
解得
(2)粒子a在进入电场后做类平抛运动，设离开电场E1时到O点的距离为L，如图所示，则
由于两粒子完全相同，所以只需在带电粒子a进入电场E1时速度方向的直线OM上任一点释放粒子b，可保证两者离开电场前碰撞。
若相遇时所需时间最长，则在M点由静止释放带电粒子b即可，则有
OM ＝ Lcos 30°
故M的横坐标为
M的纵坐标为
联立解得
即在电场E1中由静止释放带电粒子b的位置坐标为
练习册系列答案
相关题目
