Question

【题目】如图所示,水平传送带的长度L=10m,皮带轮的半径R=0.1m,皮带轮以角速度ω顺时针匀速转动。现有一小物体(视为质点)从A点无初速度滑上传送带，到B点时速度刚好达到传送带的速度,越过B点后做平抛运动,落地时物体速度与水平面之间的夹角为。已知B点到地面的高度。

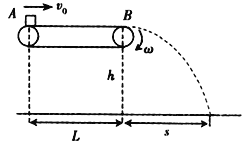
（1）小物体越过B点后经多长时间落地及平抛的水平位移S.

（2）皮带轮的角速度ω

（3）物体与传送带间的动摩擦因

Answer 1

【答案】(1) (2) (3)

【解析】试题分析：(1)由B做平抛运动，按平抛运动的处理方法，水平方向做匀速直线运动，竖直方向自由落体运动列方程求解；

(2) 由线速度与角速度的关系可求出皮带轮的角速度；

(3)根据牛顿第二定律和匀变直线运动的速度位移公式即可求解。

解：(1) 物体从B开始做平抛运动，设平抛运动时间为t，

在竖直方向上：解得：

竖直方向速度：vy=gt=10×1=10m/s

又由几何关系知水平速度：v0=vytan45°=10×1=10m/s

物体平抛运动的水平位移：s=v0t=（10×1）m=10m；

(2) 由线速度与角速度的关系可知：v=Rω

传送带角速度：；

(3) 由匀变速运动的速度位移公式得：v2-v02=2aL

解得：

对物体，由牛顿第二定律得：

所以动摩擦因数：。