Question

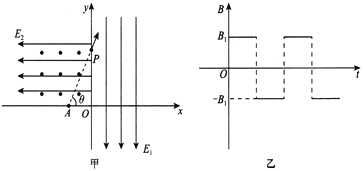
【题目】如图甲所示，绝缘水平面上固定着两根足够长的光滑金属导轨PQ、MN， 相距为L=0.5m，ef右侧导轨处于匀强磁场中，磁场方向垂直导轨平面向下，磁感应强度B的大小如图乙变化。开始时ab棒和cd棒锁定在导轨如图甲位置，ab棒与cd棒平行，ab棒离水平面高度为h=0.2m，cd棒与ef之间的距离也为L，ab棒的质量为m1=0.2kg，有效电阻R1=0.05Ω，cd棒的质量为m2=0.1kg，有效电阻为R2=0.15Ω。(设a、b棒在运动过程始终与导轨垂直，两棒与导轨接触良好，导轨电阻不计)。问：

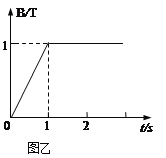
(1)0~1s时间段通过cd棒的电流大小与方向；

(2)假如在1s末，同时解除对ab棒和cd棒的锁定，稳定后ab棒和cd棒将以相同的速度作匀速直线运动， 试求这一速度；

(3)对ab棒和cd棒从解除锁定到开始以相同的速度作匀速运动，ab棒产生的热量为多少?

(4)ab棒和cd棒速度相同时，它们之间的距离为多大?

Answer 1

【答案】(1) ， (2) (3) (4)

【解析】试题分析：(1)由题意可知0~1s时间内由于磁场均匀变化，根据法拉第电磁感应定律求出感应电动势，再根据闭合电路欧姆定律求出电流；

(2)先由动能定理求出ab棒从高为h处滑下到ef的速度，再由动量守恒定律求出共同的速度；

(3) 对ab棒和cd棒从解除锁定到开始以相同的速度作匀速运动过程，由能量守恒求出总热量，再由串联电路中热量分配按电阻分配求出ab棒中的热量；

(1) 0~1s时间内由于磁场均匀变化，根据法拉第电磁感应定律和闭合电路欧姆定律，代入数据可解得： ；

(2)1s末后由磁场不变，ab棒从高为h处滑下到ef过程，由动能定理可知，

得，

从ab棒刚到ef处至两棒达共同速度过程，由动量守恒定律得，

即

解得；

(3) 对ab棒和cd棒从解除锁定到开始以相同的速度作匀速运动过程，由能量守恒可知，

代入数据解得：

由于ab和cd棒串联，所以产生的热量之比等于电阻之比，所以

。