题目内容
 物体A、B质量分别为10kg和5kg.它们由轻绳连接静止在水平面上如图所示.当B受到水平拉力F以后,该系统开始作匀加速直线运动,加速度大小为4m/s2.在第5秒末使连接A、B的绳断开,又经过20秒,A物体停止了运动,已知B与水平面的摩擦系数为0.2.(g=10m/s2)求:
物体A、B质量分别为10kg和5kg.它们由轻绳连接静止在水平面上如图所示.当B受到水平拉力F以后,该系统开始作匀加速直线运动,加速度大小为4m/s2.在第5秒末使连接A、B的绳断开,又经过20秒,A物体停止了运动,已知B与水平面的摩擦系数为0.2.(g=10m/s2)求:(1)A物体与水平面的摩擦系数;
(2)断开前绳的张力;
(3)水平外力F.
分析:(1)根据速度时间公式求出5s末的速度,再根据速度时间公式求解出减速过程的加速度,然后根据牛顿第二定律列式求解A物体与水平面的摩擦系数;
(2)对物体A整体受力分析,根据牛顿第二定律列式求解即可;
(3)对物体AB整体受力分析,然后根据牛顿第二定律列式求解即可.
(2)对物体A整体受力分析,根据牛顿第二定律列式求解即可;
(3)对物体AB整体受力分析,然后根据牛顿第二定律列式求解即可.
解答:解:(1)前5s整体向前做匀加速运动,根据速度时间公式,有
第5秒末速度 V1=at1=4×5=20 m/s
绳断后对A运用速度时间公式,有
0=V1-aAt2
解得
aA=1 m/s2
根据牛顿第二定律,有
aA=μAg
解得
μA=0.1
即A物体与水平面的摩擦系数0.1.
(2)设所求绳力是T,对A,根据牛顿第二定律,有
T-μAmAg=mAaA
解得
T=20N
故断开前绳的张力为20N.
(3)对整体受力分析,受重力、支持力、拉力和总的滑动摩擦力,根据牛顿第二定律,有
F-μAmAg-μBmBg=(mA+mB)a
解得
F=80N
即水平外力F为80N.
第5秒末速度 V1=at1=4×5=20 m/s
绳断后对A运用速度时间公式,有
0=V1-aAt2
解得
aA=1 m/s2
根据牛顿第二定律,有
aA=μAg
解得
μA=0.1
即A物体与水平面的摩擦系数0.1.
(2)设所求绳力是T,对A,根据牛顿第二定律,有
T-μAmAg=mAaA
解得
T=20N
故断开前绳的张力为20N.
(3)对整体受力分析,受重力、支持力、拉力和总的滑动摩擦力,根据牛顿第二定律,有
F-μAmAg-μBmBg=(mA+mB)a
解得
F=80N
即水平外力F为80N.
点评:本题关键是对A物体、B物体或整体受力分析,然后根据牛顿第二定律列式后联立方程组求解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图所示,物体A、B质量分别为mA、mB,用轻质弹簧相连接,弹簧的劲度系数为k,c为一固定挡板,系统处于静止状态.现给物体A施加沿斜面向上的恒力F,使物块A由静止开始沿斜面向上运动(斜面光滑且固定,重力加速度为g)求:
如图所示,物体A、B质量分别为mA、mB,用轻质弹簧相连接,弹簧的劲度系数为k,c为一固定挡板,系统处于静止状态.现给物体A施加沿斜面向上的恒力F,使物块A由静止开始沿斜面向上运动(斜面光滑且固定,重力加速度为g)求: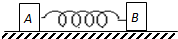 如图所示,静止在光滑水平面上的物体A和B质量分别为m和2m,它们之间用轻弹簧相连,在极短时间内对物体A作用一水平向右的冲量I,可知( )
如图所示,静止在光滑水平面上的物体A和B质量分别为m和2m,它们之间用轻弹簧相连,在极短时间内对物体A作用一水平向右的冲量I,可知( )
 B.
B. C.F
D.
C.F
D.
