题目内容
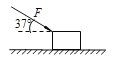
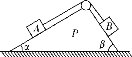
【题目】如图所示,一个截面是三角形的物体P平放在水平地面上,它的两个斜面与水平的夹角分别为α、β,且α<β,P的顶端装有一定滑轮,一轻质细绳跨过定滑轮后连接A、B二个质量相等的滑块,连接后细绳与各自的斜面平行,所有接触面都不计摩擦,重力加速度大小为g.
(1)若P固定不动,求A、B的加速度大小.
(2)若P向右做匀加速运动,加速度多大时能使A、B与斜面不发生相对滑动.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)P固定时,A、B的加速度大小相等,设为a1,以F表示绳的张力,则
滑块A:F-mgsin α=ma1
滑块B:mgsin β-F=ma1
解得:![]()
(2)设P向右的加速度为a,A、B相对斜面不发生滑动时,A、B的加速度也为a,仍用F表示绳中的张力,则:
滑块A沿斜面方向:F-mgsin α=macos α
滑块B沿斜面方向:mgsin β-F=macos β
解得:a=![]() =
=![]()

练习册系列答案
相关题目