题目内容
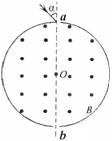
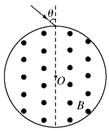
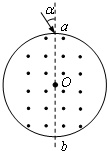如图是某离子速度选择器的原理示意图，在一半径为R=10cm的圆形筒内有B=1×10-4T的匀强磁场，方向平行于轴线．在圆柱形筒上某一直径两端开有小孔a、b分别作为入射孔和出射孔．现有一束比荷为| q |
| m |
分析：由题，离子束不经碰撞而直接从出身孔射出，即可根据几何知识画出轨迹，由几何关系求出轨迹的半径，即可由牛顿第二定律求速度v．
解答：
解：离子从小孔a射入磁场，与ab方向的夹角为α=30°，则离子从小孔b离开磁场时速度与ab的夹角也为α=30°，过入射速度和出射速度方向作垂线，得到轨迹的圆心O′，画出轨迹如图，由几何知识得到轨迹所对应的圆心角θ=2α=60°，则离子的轨迹半径r=2R
由牛顿第二定律得：
qvB=m
得v=
=2×1011×1×10-4×0.2m/s=4×106m/s
故选C
解：离子从小孔a射入磁场，与ab方向的夹角为α=30°，则离子从小孔b离开磁场时速度与ab的夹角也为α=30°，过入射速度和出射速度方向作垂线，得到轨迹的圆心O′，画出轨迹如图，由几何知识得到轨迹所对应的圆心角θ=2α=60°，则离子的轨迹半径r=2R由牛顿第二定律得：
qvB=m
| v2 |
| r |
得v=
| qBr |
| m |
故选C
点评：本题的解题关键是根据几何知识画出离子的运动轨迹，得到半径，即可求解速度v．
练习册系列答案
相关题目
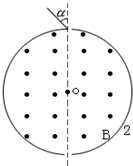（2007?苍山县模拟）如图是某离子速度选择器的原理示意图，在一半径为R=10cm的圆柱形桶内有B=10-4T的匀强磁场，方向平行于轴线，在圆柱桶某一直径两端开有小孔，作为入射孔和出射孔．离子束以不同角度入射，最后有不同速度的离子束射出．现有一离子源发射质荷比为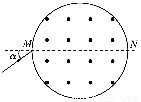
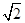×106 m/s B.2
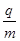=2×1011C/kg的正离子，以不同角度α入射，最后有不同速度的离子束射出.其中入射角α=30°，且不经碰撞而直接从出射孔射出的离子的速度v大小是（ ）