题目内容
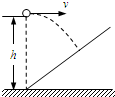 如图所示,在斜面底端的正上方h处水平越出一个物体,飞行一段时间后,垂直地撞在倾角为45°的斜面上.可知物体完成这段飞行的时间是( )
如图所示,在斜面底端的正上方h处水平越出一个物体,飞行一段时间后,垂直地撞在倾角为45°的斜面上.可知物体完成这段飞行的时间是( )分析:研究平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究,水平方向做匀速直线运动,竖直方向做自由落体运动,两个方向上运动的时间相同.
解答:解:设飞行的时间为t,
则x=V0t
OQ=
gt2
因为是垂直装上斜面,斜面与水平面之间的夹角为45°,所以在P点水平速度和竖直方向速度相等,
即:V0=gt
因为斜面与水平面之间的夹角为45°,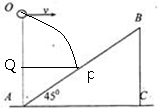 如图所示,
如图所示,
由三角形的边角关系可知,
AQ=PQ
所以在竖直方向上有,
OQ+AQ=h
所以 V0t+
gt2=h
解得:t=
故选A.
则x=V0t
OQ=
| 1 |
| 2 |
因为是垂直装上斜面,斜面与水平面之间的夹角为45°,所以在P点水平速度和竖直方向速度相等,
即:V0=gt
因为斜面与水平面之间的夹角为45°,
 如图所示,
如图所示,由三角形的边角关系可知,
AQ=PQ
所以在竖直方向上有,
OQ+AQ=h
所以 V0t+
| 1 |
| 2 |
解得:t=
|
故选A.
点评:该题是平抛运动基本规律的应用,主要抓住撞到斜面上时水平速度和竖直方向速度的关系以及位移的关系解题,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
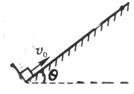 在倾角为θ=30°的足够长的斜面底端,木块A以某一初速度v0沿斜面向上运动,若木块与斜面间的动摩擦因数μ=
在倾角为θ=30°的足够长的斜面底端,木块A以某一初速度v0沿斜面向上运动,若木块与斜面间的动摩擦因数μ=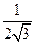 ,g取10m/s2,试求:
,g取10m/s2,试求:

 B.
B. C.
C. D.条件不足,无法计算
D.条件不足,无法计算