题目内容
(15分)如图所示，质量为M＝2kg的木板B静止在光滑水平面上，质量为m＝1kg可视为质点的木块A以水平速度v0＝2m/s从右端向左滑上木板，木块与木板间的动摩擦因数为μ＝0.5，此时有一水平向右的力F＝10N作用在长木扳上，g取10m/s2。
⑴求开始时木块A和木板B各自的加速度大小；
⑵若木板足够长，求从木块滑上木板到木块和木板速度相等所经历的时间；
⑶要使木块不从木板上滑落，求木板的最小长度。
⑴求开始时木块A和木板B各自的加速度大小；
⑵若木板足够长，求从木块滑上木板到木块和木板速度相等所经历的时间；
⑶要使木块不从木板上滑落，求木板的最小长度。
⑴aA＝5m/s2，aB＝2.5m/s2；⑵t＝0.8s；⑶Δx＝0.8m。
试题分析：⑴开始时，对木块A，受重力mg、木板的支持力NA和水平向右的滑动摩擦力fA作用，根据牛顿第二定律可知，在水平方向上有：fA＝maA ①
在竖直方向上有：NA－mg＝0 ②
根据滑动摩擦定律有：fA＝μNA ③
由①②③式联立解得：aA＝μg＝5m/s2
对木板B，受水平向右的力F、重力Mg、地面的支持力NB、木块的压力NA′和水平向左的滑动摩擦力fA′作用，根据牛顿第二定律可知，在水平方向上有：F－fA′＝MaB ④
根据牛顿第三定律有：fA′＝fA ⑤
由②③④⑤式联立解得：aB＝
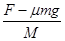＝2.5m/s2⑵由⑴中分析可知，木块开始在木板上向左做匀减速直线运动，设经时间t1速度减为零，木板则向右做匀加速直线运动，根据匀变速直线运动规律可知，对A有：t1＝
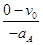＝0.4s ⑥此时，木块在木板的摩擦力作用下，将开始向右做匀加速直线运动，设经过时间t2与木板具有了相同速度v，根据匀变速直线运动规律可知，对A有：v＝aAt2 ⑦
从木块开始滑上木板到两者具有相同速度的过程中，木板B的运动状态不变，有：v＝aB(t1＋t2) ⑧
由⑥⑦⑧式联立解得从木块滑上木板到木块和木板速度相等所经历的时间为：t＝t1＋t2＝0.8s
⑶由⑵中分析可知，在t1时间内，木块A向左运动的位移为：xA1＝
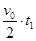＝0.4m在t2时间内，木块A向右运动的位移为：xA2＝
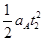＝0.4m在整个t时间内，木板B向右运动的位移为：xB＝
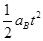＝0.8m在整个t时间内，木块A始终相对木板B向左运动，其相对位移为：Δx＝xB＋xA1－xA2＝0.8m
因此要使木块不从木板上滑落，木板的最小长度为：Δx＝0.8m
练习册系列答案
相关题目
），长途客车的“速度－时间”图象如图（乙）所示，求：
L/2
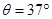，以5 m/s的恒定速度向上运动。一个质量为2 kg的物块（可视为质点），沿平行于传送带方向以10 m/s的速度滑上传送带，已知物块与传送带之间的动摩擦因数μ=0.5，sin370=0.6,cos370=0.8,g=10m/s2。求：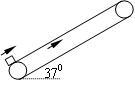
，警车发动起来，以加速度
做匀加速运动，试问：