题目内容
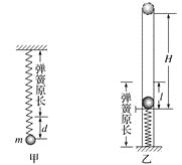
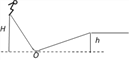
【题目】如图所示,一质量为m的极限滑雪运动员自高为H的雪山顶端由静止下滑,经圆弧(通过时忽略能量损失,并且时间极短)状底端O后,恰能滑至右侧高为h的平台上。已知H>h,且下滑的路程小于上滑的路程。忽略空气阻力,雪道各处的粗糙程度相同,下滑和上滑视为直线运动,重力加速度为g,则在整个运动过程中
A. 运动员克服摩擦力做的功为mg(H-h)
B. 运动员下滑过程所用的时间较短
C. 运动员重力势能减少量为mgH
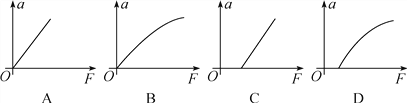
D. 运动员的机械能与通过的路程呈线性关系
【答案】ABD
【解析】A、根据动能定理可知,整个过程中有![]() ,解得:
,解得:![]() ,故选项A正确;
,故选项A正确;
B、由牛顿第二定律和运动学规律有![]() ,因运动员下滑的末速率等于上滑的初速率且下滑过程的路程小于上滑过程的路程,得a下>a上,又v=at,可得下滑时间小于上滑时间,选项B正确;
,因运动员下滑的末速率等于上滑的初速率且下滑过程的路程小于上滑过程的路程,得a下>a上,又v=at,可得下滑时间小于上滑时间,选项B正确;
C、整个过程中,运动员重力势能的减少量等于ΔEp= mg(H-h),选项C错误;
D、由机械能守恒可得![]() ,
,![]() 图线的斜率代表其除重力和系统内弹力以外的其他力,即摩擦力,由于下滑和上滑过程中,摩擦力都是一定的,得出的函数关系图象都是直线,选项D正确。
图线的斜率代表其除重力和系统内弹力以外的其他力,即摩擦力,由于下滑和上滑过程中,摩擦力都是一定的,得出的函数关系图象都是直线,选项D正确。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
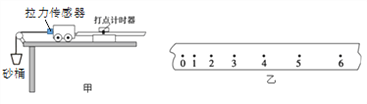
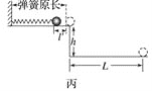
【题目】某实验小组用如图所示的装置测量弹簧的劲度系数k。每当挂在弹簧下端的钩码(每个钩码质量m=50g)处于静止状态时,用刻度尺测出对应的弹簧长度L(弹簧始终在弹性限度内),列表记录如下:
所挂钩码个数n | 1 | 2 | 3 | 4 | 5 | 6 |
| 10.18 | 13.09 | 14.58 | 16.08 | 17.54 |

(1)表格中第二组数据的弹簧长度如图示,则弹簧长度为________cm;
(2)用所学知识尽量精确计算出每挂一个钩码弹簧伸长量ΔL=__________cm;并由ΔF=kΔL算出弹簧的劲度系数k=_______N/m.(g=9.8m/s,结果保留位有效数字)