题目内容
15. 如图所示,竖直平面被分为足够长的I、II两个区域,这两个区域有垂直于竖直平面向里的匀强磁场,磁感应强度均为B.I区固定有竖直放置的平行金属薄板K、K′,极板间距离为d.II区用绝缘装置竖直固定两根电阻可忽略的金属导轨,导轨间距离为l,且接有阻值为R的电阻,导轨与金属板用导线相连.电阻为r、长为l的导体棒与导轨接触良好,在外力作用下沿导轨匀速向上运动.一电荷量为q、质量为m的带负电的小球从靠近金属板K的A处射入I区,射入时速度在竖直平面内且与K板夹角为45°,在板间恰能做直线运动.(重力加速度为g)
如图所示,竖直平面被分为足够长的I、II两个区域,这两个区域有垂直于竖直平面向里的匀强磁场,磁感应强度均为B.I区固定有竖直放置的平行金属薄板K、K′,极板间距离为d.II区用绝缘装置竖直固定两根电阻可忽略的金属导轨,导轨间距离为l,且接有阻值为R的电阻,导轨与金属板用导线相连.电阻为r、长为l的导体棒与导轨接触良好,在外力作用下沿导轨匀速向上运动.一电荷量为q、质量为m的带负电的小球从靠近金属板K的A处射入I区,射入时速度在竖直平面内且与K板夹角为45°,在板间恰能做直线运动.(重力加速度为g)(1)求导体棒运动的速度v1;
(2)若只撤去I区磁场,其它条件不变,要使小球刚好到达K′板上正对A的位置A′,极板间距离d应满足什么条件?
分析 (1)带负电的小球在板间恰能做直线运动,由于洛伦兹力与速度成正比,可知小球必定做匀速直线运动,分析其受力情况,由平衡条件和法拉第电磁感应定律、欧姆定律结合求解.
(2)若只撤去I区磁场,小球在电场力和重力的作用下做类平抛运动,运用运动的分解法,由牛顿第二定律和运动学公式结合解答.
解答 解:(1)由题分析知小球在板间做匀速直线运动,受力分析如图所示.
有qE=mg
设竖直两板的电压为U.
根据法拉第电磁感应定律、欧姆定律有:
Blv1=$\frac{U}{R}$(R+r)
另有U=Ed
解得 v1=$\frac{mgd(R+r)}{BlqR}$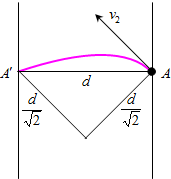
(2)撤去I区磁场,对小球进行受力分析,可知小球做类平抛运动.
设从A到A'的时间为t,加速度为a.
在合外力方向上,有 $\frac{d}{\sqrt{2}}$=$\frac{1}{2}a{t}^{2}$
初速度v2方向上,有 $\frac{d}{\sqrt{2}}$=v2t
根据上题得 F合=Bqv2=$\sqrt{2}$mg
由牛顿第二定律,有 F合=ma
解得 d=$\frac{4{m}^{2}g}{{B}^{2}{q}^{2}}$
答:
(1)导体棒运动的速度v1为$\frac{mgd(R+r)}{BlqR}$.
(2)要使小球刚好到达K′板上正对A的位置A′,极板间距离d应满足的条件是d=$\frac{4{m}^{2}g}{{B}^{2}{q}^{2}}$.
点评 解决本题的关键要正确分析小球的受力情况和运动情况,熟练运用运动的分解法处理类平抛运动.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.以下说法正确的是( )
| A. | 已知阿伏加德罗常数、气体摩尔质量和密度,可算出该气体分子间的平均距离 | |
| B. | 为了保存玉米地的水分,可以锄松地面,破坏土壤里的毛细管 | |
| C. | 随着分子间距离的增大,分子间的引力和斥力都减小,但斥力减小得快,合力表现为引力 | |
| D. | 物质是晶体还是非晶体,比较可靠的办法是从各向异性或各向同性来判断 | |
| E. | 能量耗散从能量角度反映出自然界的宏观过程具有方向性 |
10. 2015年1月10日广元航模协会在广元中学运动场举行了盛大的航模表演,像“空中芭蕾”、“8字穿越”、“直升飞机倒飞悬停”、“彩虹”等节目令同学们大开眼界.则( )
2015年1月10日广元航模协会在广元中学运动场举行了盛大的航模表演,像“空中芭蕾”、“8字穿越”、“直升飞机倒飞悬停”、“彩虹”等节目令同学们大开眼界.则( )
 2015年1月10日广元航模协会在广元中学运动场举行了盛大的航模表演,像“空中芭蕾”、“8字穿越”、“直升飞机倒飞悬停”、“彩虹”等节目令同学们大开眼界.则( )
2015年1月10日广元航模协会在广元中学运动场举行了盛大的航模表演,像“空中芭蕾”、“8字穿越”、“直升飞机倒飞悬停”、“彩虹”等节目令同学们大开眼界.则( )| A. | 航模飞机在竖直平面内做圆周运动时,在最低点机舱内的零件处于超重状态 | |
| B. | 航模飞机的遥控装置与电视机遥控板一样,都是利用了红外线的特性 | |
| C. | 航模飞机释放的彩色烟雾形成的彩虹与雨后的彩虹原理不同,雨后的彩虹是光的反射形成的 | |
| D. | 直升机悬停时,螺旋桨对空气的力向下,直升机倒飞悬停时,螺旋桨对空气的力向上 |
20.某一单色光在真空中的波长为λ0、频率为v0,在水中的波长为λ、频率为v.则水对该单色光的折射率n为( )
| A. | $\frac{{λ}_{0}}{λ}$ | B. | $\frac{λ}{{λ}_{0}}$ | C. | $\frac{{v}_{0}}{v}$ | D. | $\frac{v}{{v}_{0}}$ |
7. 如图,斜面C放置在水平面上,小物体B放置在C上,小球A用细线跨过光滑定滑轮与B相连,B与滑轮间的细线保持竖直方向.将A向左拉至一定高度(低于滑轮)由静止释放,使A在竖直平面内摆动,在A摆动过程中,B、C始终保持静止.则( )
如图,斜面C放置在水平面上,小物体B放置在C上,小球A用细线跨过光滑定滑轮与B相连,B与滑轮间的细线保持竖直方向.将A向左拉至一定高度(低于滑轮)由静止释放,使A在竖直平面内摆动,在A摆动过程中,B、C始终保持静止.则( )
 如图,斜面C放置在水平面上,小物体B放置在C上,小球A用细线跨过光滑定滑轮与B相连,B与滑轮间的细线保持竖直方向.将A向左拉至一定高度(低于滑轮)由静止释放,使A在竖直平面内摆动,在A摆动过程中,B、C始终保持静止.则( )
如图,斜面C放置在水平面上,小物体B放置在C上,小球A用细线跨过光滑定滑轮与B相连,B与滑轮间的细线保持竖直方向.将A向左拉至一定高度(低于滑轮)由静止释放,使A在竖直平面内摆动,在A摆动过程中,B、C始终保持静止.则( )| A. | 斜面C对水平面的静摩擦力可能向右 | |
| B. | 小物体B所受静摩擦力方向可能沿斜面向下 | |
| C. | 小物体B所受静摩擦力可能为零 | |
| D. | 斜面C对水平面的压力可能等于B、C重力之和 |
5.如图所示,两束单色光a,b分别照射到玻璃三棱镜AC面上,穿过三棱镜后互相平行,则( )


| A. | a光的折射率大 | B. | b光的折射率大 | ||
| C. | a光在三棱镜中的速度大 | D. | b光在三棱镜中的速度大 |
 如图所示,空气中有一底面半径为R的圆柱形容器,在底面的中心O处有一红色点光源S,它发出的红光经时间t可以传到容器的边缘P,若容器内盛满某透明液体,S发出的红光经过时间2t可以传到容器的边缘P,且恰好在P点发生全反射.求该液体对红光的折射率n和容器的高度h.
如图所示,空气中有一底面半径为R的圆柱形容器,在底面的中心O处有一红色点光源S,它发出的红光经时间t可以传到容器的边缘P,若容器内盛满某透明液体,S发出的红光经过时间2t可以传到容器的边缘P,且恰好在P点发生全反射.求该液体对红光的折射率n和容器的高度h. 如图所示,位于原点O处的波源在t=0时刻,从平衡位置(在x轴上)开始沿y轴正方向做周期T=0.4s、振幅A=3cm的简谐运动,该波源产生的简谐横波沿x轴正方向传播,当平衡位置坐标为(6m,0)的质点P刚开始振动时波源刚好位于波谷.
如图所示,位于原点O处的波源在t=0时刻,从平衡位置(在x轴上)开始沿y轴正方向做周期T=0.4s、振幅A=3cm的简谐运动,该波源产生的简谐横波沿x轴正方向传播,当平衡位置坐标为(6m,0)的质点P刚开始振动时波源刚好位于波谷. 用如下的器材和方法可以验证“力的平行四边形定则”.在圆形桌子桌面平铺一张白纸,在桌子边缘安装三个光滑的滑轮,其中,滑轮P1固定在桌子边,滑轮P2、P3可沿桌边移动.第一次实验中,步骤如下:
用如下的器材和方法可以验证“力的平行四边形定则”.在圆形桌子桌面平铺一张白纸,在桌子边缘安装三个光滑的滑轮,其中,滑轮P1固定在桌子边,滑轮P2、P3可沿桌边移动.第一次实验中,步骤如下: